Independent Projects
Tilings of the Hyperbolic Plane
Mentor: Anna Schilling
Team members: Yes
Ray Marching in Translation Surfaces

Mentor: Diaaeldin Taha
Team members: Fabian Lander, Mara-Eliana Popescu
Description: A translation surface is a surface obtained by gluing together a finite collection of polygons in the Euclidean plane along parallel sides of the same length. In this project, we develop an immersive visualization of the geometry of translation surfaces (and mirror rooms, and surfaces of polyhedra) with raymarching.
GitHub: link
Online app: link
SFB Funded Projects
Symplectic Billiards
Mentor: Peter Albers
Team members: Fabian Lander, Jannik Westermann
Description: The goal of this project is to simulate symplectic billiards on non-convex polygons, and to search for periodic orbits in particular.
Hyperbolic Billiards
Mentor: Diaaeldin Taha
Team members: Jannis Heising, Mara-Eliana Popescu
Details: The project aims to study closed billiard trajectories in hyperbolic polygons.
GitHub: link
HEGL Proseminar/Seminar: Illustrating Mathematics
2D Hyperbolic Game Engine
Mentor: Valentina Disarlo, Diaaeldin Taha
Team members: Ines Bultmann, Filippa Piazolo
Details: In this project, we will create a 2D hyperbolic geometry game engine that implements basic features such as free motion, collision detection, and portals. Using our game engine, we will build hyperbolic analogues of some classical arcade games like Combat (1977) and Asteroids (1979).
GitHub: link
Blog post: link
Online app: link 1 (1vs1), link 2 (single player)
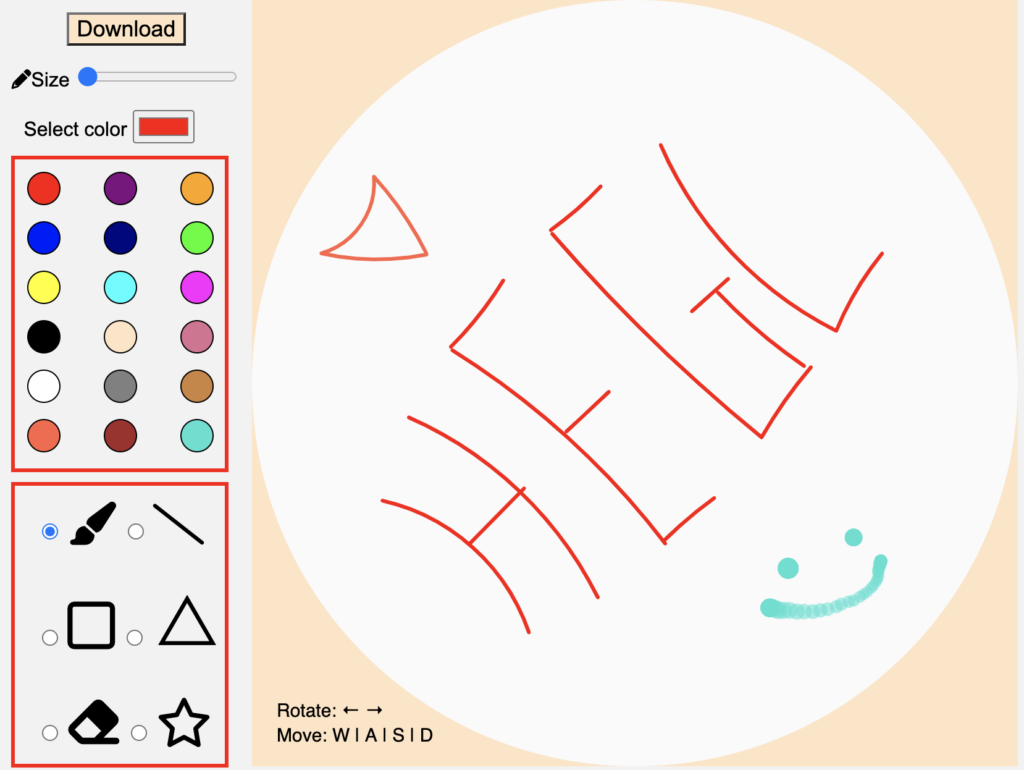
Möbius Paint
Mentor: Diaaeldin Taha
Team members: Mouna Dorothea Deubler, Yunus Sahin, Juliane Stehle
Details: This project aims to build a hyperbolic analogue of simple graphic editors such as MacPaint (1984) and Microsoft Paint (1985). Our editor will implement drawing features such as brushes and “straight lines” (i.e., geodesics) and canvas operations such as reflections, rotations, and translations.
GitHub: link
Online app: link
Hopf Fibration

Mentor: Diaaeldin Taha
Team members: Carola Behr, Burak Ertan, Jonas Hoecht
Details: This project aims to artistically visualize the Hopf fibration using several media such as 3D printing, interactive computer graphics, and photo-realistic rendering.
GitHub: link
Blog post: link
Indra’s Pearls

Mentor: Diaaeldin Taha
Team members: Alassane Diagne, Aysegül Peközsoy
Details: The goal of this project is to investigate the geometry and dynamics of Möbius transformation with computer graphics following the beautiful book “Indra’s Pearls”.
GitHub: link
Online app: link
Mirrors I
Mentor: Diaaeldin Taha
Team members: Nagdakeba Bauer, Miriam Malcherek
Details: In this project, we will explore some properties of reflection groups in two and three dimensions using actual mirrors cut with our laser engraver. Possible applications include illustrating two-dimensional polygonal billiards and three-dimensional polyhedral kaleidoscopes.
BOGY-Internships
Games of Chance and Skill
Mentors: Anna Schilling, Diaaeldin Taha
Team members: Max Dörich (DBG Eppelheim), Lukas Kühlwein (DBG Eppelheim)
Details: This project aims to introduce the interns to the mathematics of games of chance and skill using computer explorations. During the first week, we will study the game SET using algebra, geometry, combinatorics, and computer simulations. During the second week, we will learn about the Sprague–Grundy theorem, and how to write programs that play famous impartial games perfectly.
GitHub: link
