HEGL Praktika
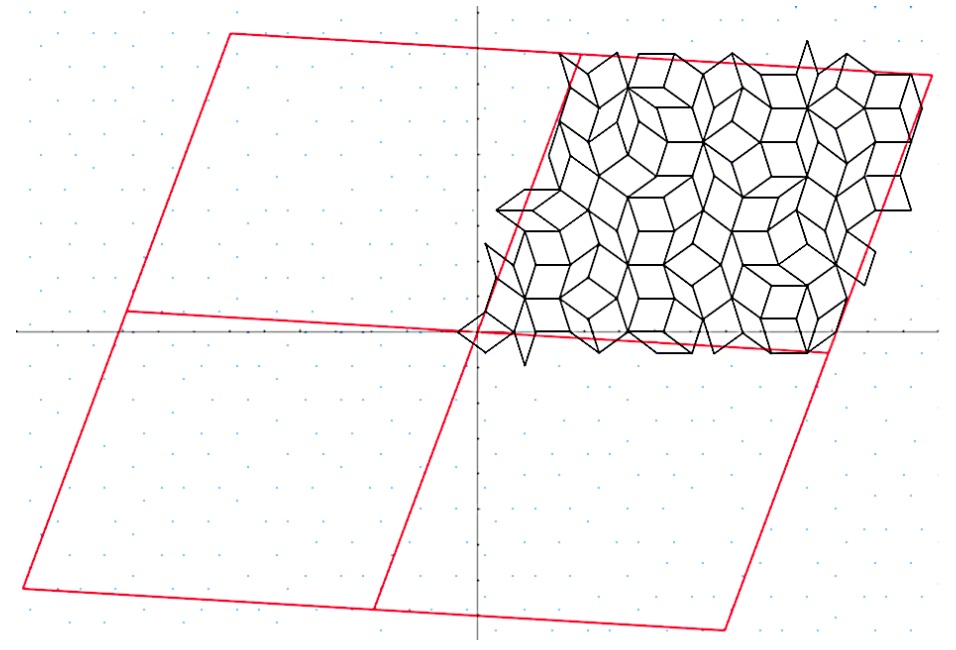
Penrose Tilings of Closed Surfaces
Mentor: Peter Smillie
Members: Alexander Baucke
Description: Penrose tiles are the most famous examples of a set of tiles which can tile the plane, but cannot tile the plane periodically. Equivalently, there can be no Penrose tiling of a flat torus. However, it is sometimes possible to tile a flat surface of higher genus. In this project, we will work towards developing an atlas of which flat surfaces can be Penrose tiled and which cannot. The primary method is a version of the cut-and-project method developed by De Bruijn in 1981; an alternative method is a version of the combinatorial method of Hurwitz. If the project is successful, it should help understand some open problems.
Prerequisites: Basic familiarity with programming, for example, in Python, is helpful.
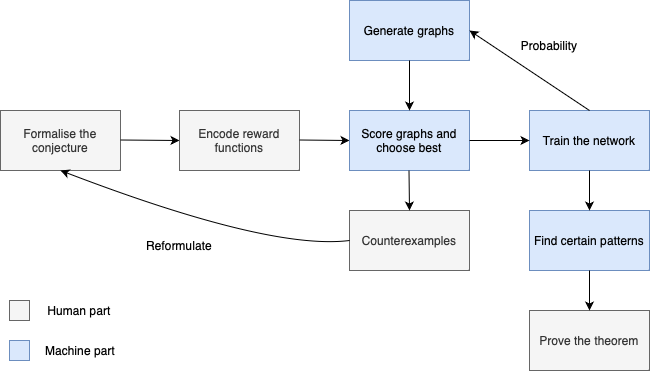
Using Reinforcement Learning to Find Counterexamples in Mathematics
Mentor: Diaaeldin Taha
Members: Hugo Hager Fernández, Karl Schamel, Chenyi Yang
Description: In a beautiful 2021 paper, Adam Wagner used reinforcement learning to find explicit constructions and counterexamples to several previously open conjectures in combinatorics. In this project, and following Wagner’s work, we will learn about reinforcement learning and how to set up some mathematical questions as problems that can be attacked with reinforcement learning.
Prerequisites: Basic programming knowledge, particularly Python, will be helpful. Familiarity with deep learning is a plus.
Bachelor Theses
Leniabreeder
Mentor: Diaaeldin Taha
Members: Adrian Becker
Description: TBA
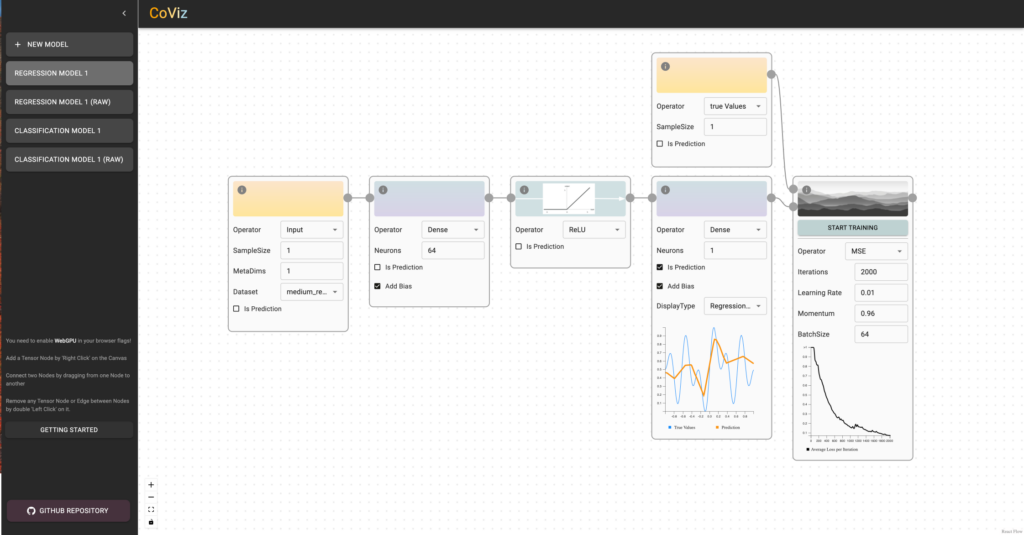
DiCo & CoViz
Mentor: Diaaeldin Taha
Members: Tillmann Fehrenbach
Description: TBA
GitHub: link
Online app: link
SFB Funded Projects
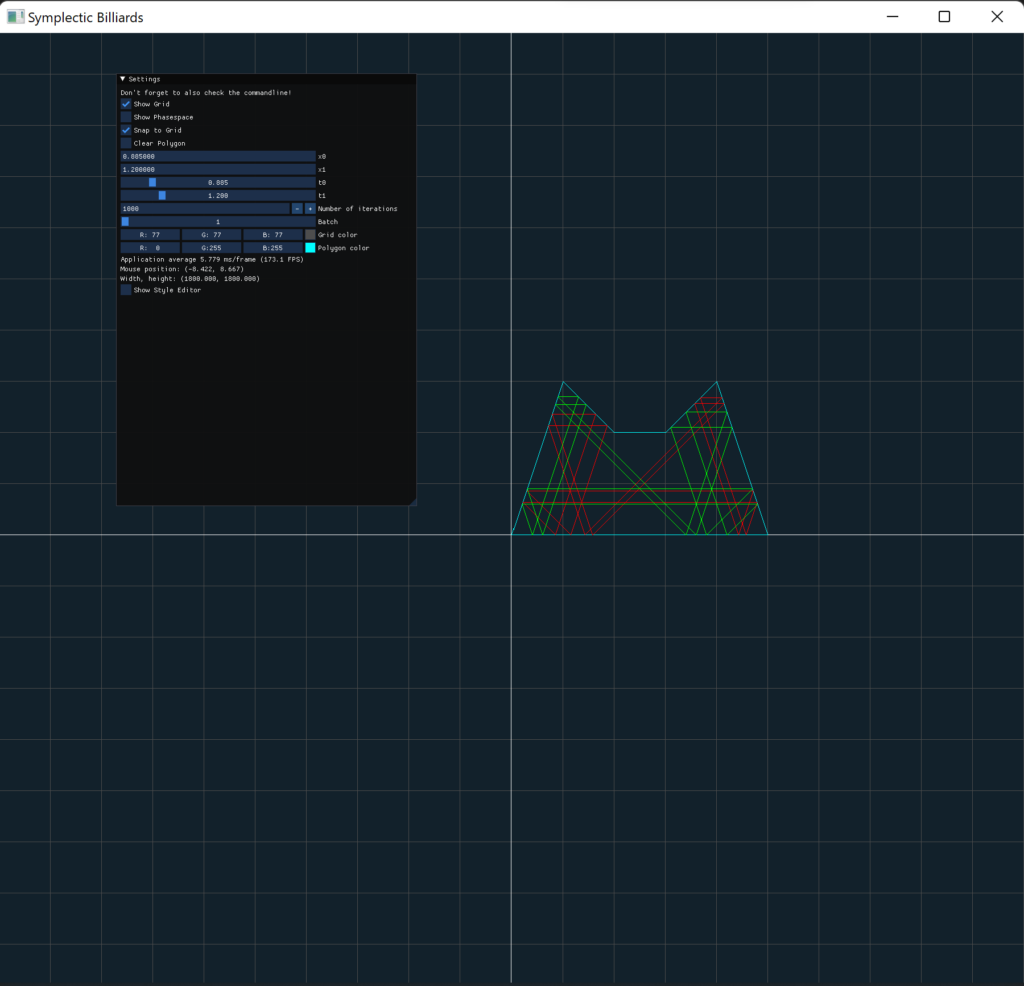
Symplectic Billiards
Mentor: Peter Albers
Members: Fabian Lander, Jannik Westermann
Description: This project aims to simulate symplectic billiards on non-convex polygons and to search for periodic orbits in particular.
HEGL Proseminar/Seminar: Illustrating Mathematics
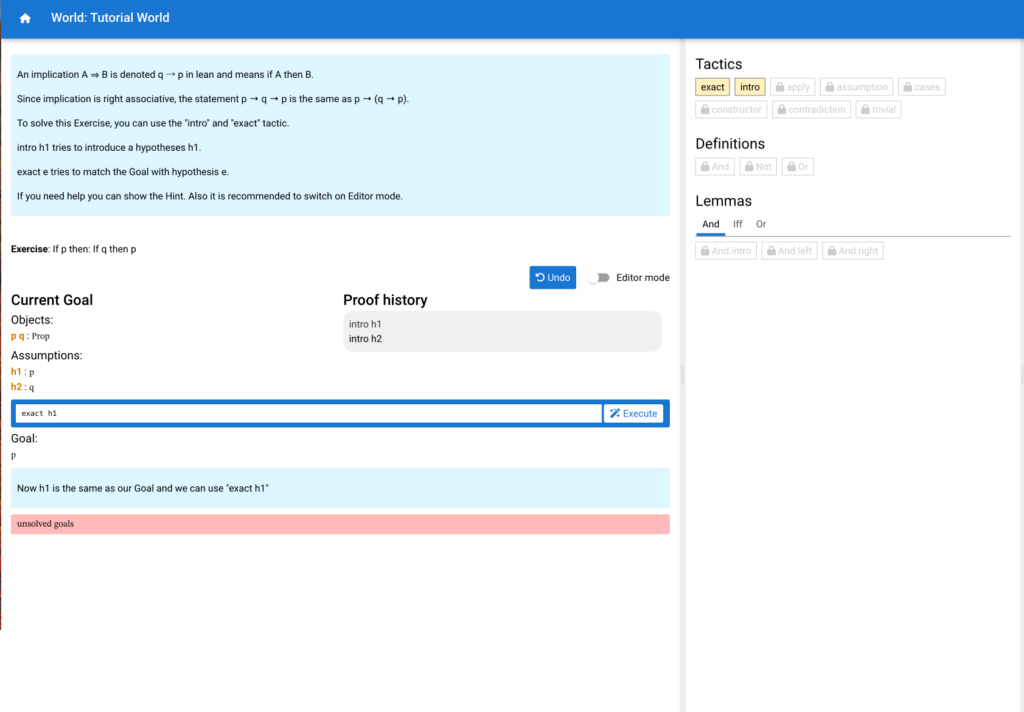
Theorem Proving with Lean
Mentor: Diaaeldin Taha
Members: Nikita Grimm, Sebastian Meier, Frederick Vandermoeten
Description: Lean is an increasingly popular theorem prover used to assist with developing formal proofs through human-machine collaboration. In this project, we will learn how to use Lean and explore its applications in research mathematics, mathematics education, and formal specification and verification.
Github: link
Blog post: link
Video presentation: link
Online app: link
Mathematical Board Games
Mentor: Diaaeldin Taha
Members: Julia Bulitta, Alina Czasch, Hanna Heer, Tadeus Pindl, Fabian Walliser
Video presentation: link
Blog post: link
Math and Art
Mentor: Diaaeldin Taha
Members: Bastian Hirschfeld, Heidi Rhodes James, Arjan Siddhpura, Ioana Todosi
Description: In this project, we will use computer generative art techniques for illustrating works at the intersection of mathematics and art. In particular, we will write software for generating recreations of the Broadway Boogie Woogie painting, Piet Mondrian’s last unfinished work.
Github: link
Blog post: link
Video presentation: link
Online app: link

Building Muqarnas
Mentor: Diaaeldin Taha
Members: Almoatasembellah Haggag
Description: The Mihrab (a concave niche situated in the wall of a mosque facing Mecca. [3]) of the 15th-century Badr al-Dın al-Aynı Madrasa in Cairo, renowned for its significance and uniqueness in the medieval city of Cairo, Egypt, was tragically lost in 1980 due to a structural collapse. This mihrab, an exemplar of artistic mastery, featured an exceptional instance of muqarnas – a distinctive form of stalactite vaulting with numerous smaller cells arranged in a complex geometric pattern to create a unified composition.
In this report, I will provide a concise discussion of the process of reconstructing a 3D model of the muqarnas vaulting. This reconstruction is based on photographs taken of the mihrab in the 20th century, as well as a set of illustrations and sketches created by the French orientalist Jules Bourgoin in the 19th century.
Blog post: link
Video presentation: link

Mirrors II
Mentor: Diaaeldin Taha
Members: Nick Bohlender, Nico Hatjigeorgiou, Carl Walter
Description: In this project, we will explore some properties of reflection groups in two and three dimensions using laser-cut mirrors. Possible applications include illustrating two-dimensional polygonal billiards and three-dimensional polyhedral kaleidoscopes.
Internships
Playing Games with NEAT
Mentor: Diaaeldin Taha, Adrian Becker
Members: Max Dörich (DBG Eppelheim), Lukas Kühlwein (DBG Eppelheim)
Description: TBA
