Written by: Julia Bulitta, Alina Czasch, Hanna Heer, Tadeus Pindl, Fabian Walliser
1. Introduction








During this past summer semester, we dealt with the task to construct a game which has mathematical knowledge. There are already many games that have mathematical knowledge. Such as card games like SET or Dobble. However, these games are easy to play for all people (like people, who have no idea about this mathematical concepts like children), as the math behind these games is often not noticed.
Below there is a small excursion into the game SET, where it is explained how much math can be behind such a simple game:
In the game SET you need to find a SET. A SET consists of exactly three cards, for which the card properties (color, shape, shading and number) must meet certain requirements. Each property has three possibilities: one, two or three for number, red, green or purple for color, ovals, squiggles or diamonds for shape and solid, stripe or open for shading. Because there is a card for each and every combination of possibilities of characteristics, we have a total of three elevated by the power of four is equal to eighty-one cards. For a SET each property must be either exactly the same three times or completely different three times on the three cards. For example, three cards with a oval or three of the same suit and filled symbols and increasing number of shapes. The mathematical background of the game is in the different properties of the cards.
To better explain the mathematical background behind the game we need to transfer the SET cards into a coordinate system. The cards can be sorted after the different properties and so we create equivalence classes for each property and each possibility. Each property has three different forms and so three equivalence classes. Each card can be described by a vector, which has the coordinates: number, color, shape and shading. For the different possibilities we assign the coordinate zero to the first possibility of the property. To the second possibility of the property we assign the coordinate one and to the third possibility of the property we assign the coordinate two. We are in the field F three elevated by the power of four. For simplified representation in the coordinate system we use the values minus one, zero and one instead of the values zero, one and two. To illustrate this, let’s look at a card that has two green elements that are solid and oval. It can be used as a vector (zero for the number of elements, zero for the color, one for shading and 1 for the shape). Now we want to take a look at a SET. The three cards of the SET have the vectors (minus one, zero, minus one, minus one), (zero, one, zero, minus one) and (one, minus one, one, minus one). For a better representation, we leave out the last property the form and go into the three dimensional. In the F three elevated by the power of three and can transfer the vectors into a coordinate system. The three cards form a SET if all three vectors form a straight line. They are collinear. Collinear means if three points a, b and c from F three high d satisfy the equation \(a + b + c = 0\). This is the case in our example.
For our own game we used the art gallery problem, which will be explained below.
2. The art gallery problem
The art gallery problem, also known as the museum problem, stands as a prominent and extensively examined visibility issue within the domain of computational geometry. The practical inspiration behind this problem lies in the realm of security and surveillance. Therefore, the task of installing surveillance cameras, guards or sensors in larger indoor areas corresponds to the mathematical challenge of examining the intricacies of visibility in polygons and line-of-sight constraints. In addition, this problem will also form the foundation and inspiration of our board game, but first of all we will explain what the mathematical side has to offer in terms of theorems and solution approaches:
The art gallery problem: Given an art gallery, what is the smallest quantity of stationary guards required to ensure the room’s protection?
In the geometric rendition of this challenge, the configuration of the art gallery finds its representation in a simple polygon, which is a connected closed region whose boundary is defined by a finite number of line segments. The position of a guard is symbolized by a point within the polygon. A collection of such points, denoted as set \(S\), is considered a covering set for a polygon if, for any point \(p\) within the polygon, there exists a point \(q\in S\) such that the line segment connecting \(p\) and \(q\) remains confined within the polygon’s boundaries.
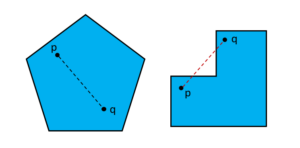
In 1973, Václav Chvátal first succeeded to prove that \(\lfloor{n\over3}\rfloor\) guards are enough and sometimes necessary to guard the museum, given there are \(n\) vertices in the polygon. However, we will now demonstrate Steve Fisk’s far less complex proof from 1978 using triangulation for better visualization:
Theorem 1: \(\lfloor{n\over3}\rfloor\) guards are occasionally necessary and always sufficient to cover a planar simple polygon with n vertices.
Base case examples (only one guard necessary):


To generalize this for an \(n\)-vertex polygon, we will use the following claims without proving them:
Claim 1: A planar simple polygon with \(n\) vertices can be triangulated with exactly \(n-2\) triangles.
Claim 2: The graph produced upon triangulation is \(3\)-colorable.
Proof:
Lower bound:
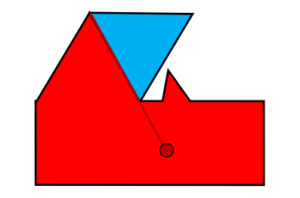
In a first step we use claim 1 to triangulate the planar simple polygon. This results in a graph whose vertices are 3-colored according to claim 2. Now it is quite obvious that a triangle under a 3-coloring must have each of the three colors since each vertex is connected to the other two vertices. Thus, each triangle has each of the 3 colors, which means that a set formed from the vertices of one of the colors completely covers the polygon, because one guard at either edge is always enough to cover a single triangle. For the final set we choose the one with the fewest vertices, so that the result is a set \(S\) with \(|S| = \lfloor {n \over 3}\rfloor\), since the three colours partition the \(n\) vertices of the polygon.
Upper bound: A simple example suffices to show that in some cases it is obligatory to have at least \(\lfloor {n \over 3}\rfloor\) elements in \(S\):
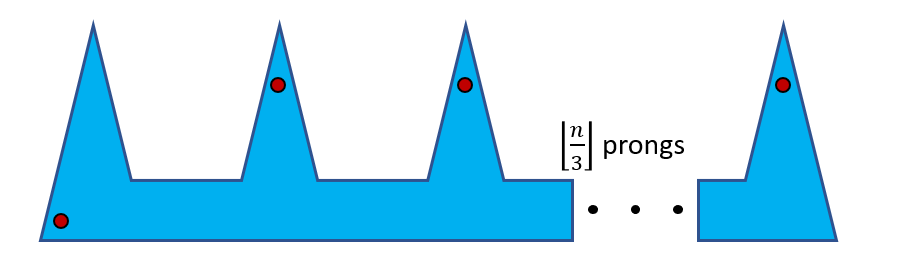
Illustration of the method using an example polygon:

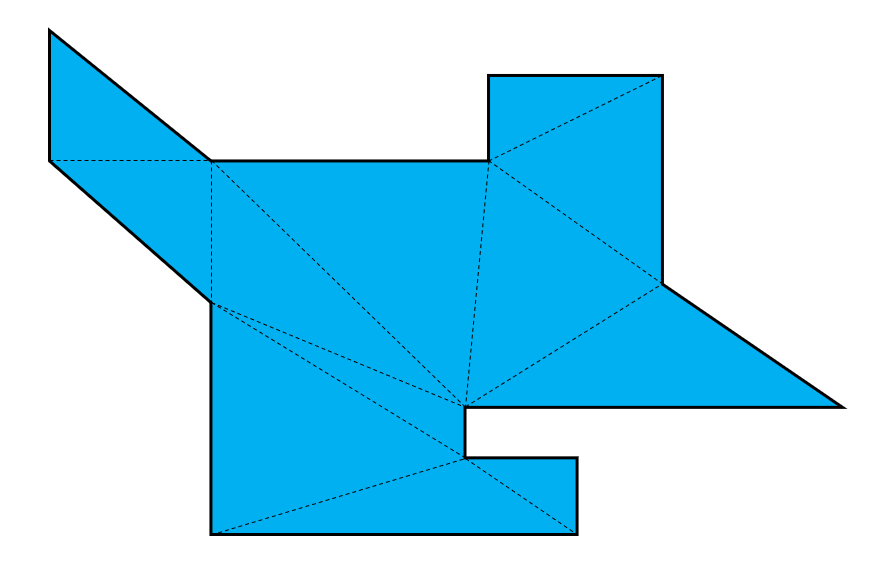
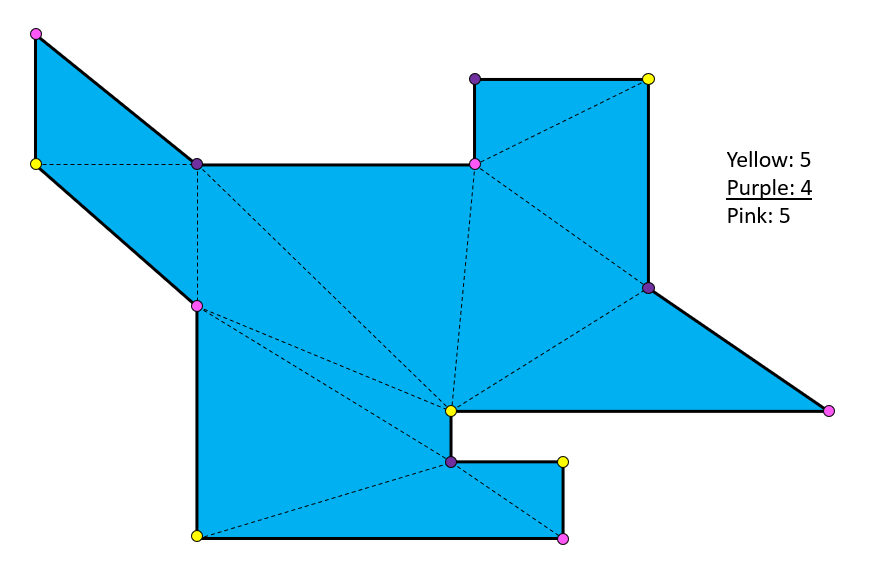
Orthogonal polygons:
Since we only use square fields in our board game, we can even come up with a tighter estimate for the number of guards needed in our museum because we are now working with an orthogonal polygon. These are polynomials that only have internal angles of \({\pi \over 2}\) (90°) or \({3\pi \over 2}\) (270°).
Theorem 2 (Kahn, Klawe and Kleitman, 1980): \(\lfloor {n \over 4}\rfloor\) guards are sufficient and sometimes necessary to cover a simple orthogonal polygon of \(n\) vertices.
The proof is very similar to Theorem 1, so we only visualize the process with an example:

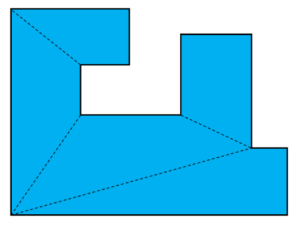
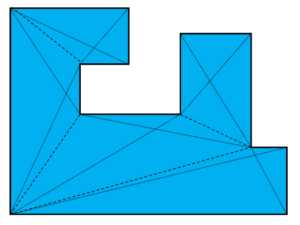
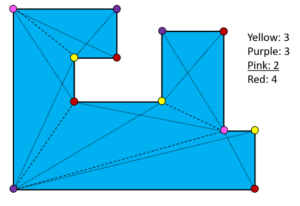
Furthermore, we observe that the board of our game is not quite a simple polygon, as it contains holes. As a matter of fact, this does not change our previously observed upper bound, so interestingly it is completely independent of the number of holes.
Theorem 3 (Hoffmann, 1990): \(\lfloor {n \over 4}\rfloor\) guards are sufficient to cover an orthogonal polygon of \(n\) vertices with \(h\) holes.
After all, it would make little sense to cover the entire area in a game where a large part of the game consists of hiding from the guards. Therefore, the upper limit of guards was not used but reduced to an enjoyable number, but the upper limit can still be calculated.
3. Development of our game idea
Once we had agreed to take this theorem as the basis for our game, the invention phase began. First, we needed a suitable museum playing field, which, according to the art gallery problem, should be a simple planar polygon. For this purpose, we drew a playing field and filled it with small circles that served as fields. We also divided it into 5 sections. With the help of the theorem, we calculated the optimal number of guards needed to overlook the whole museum.
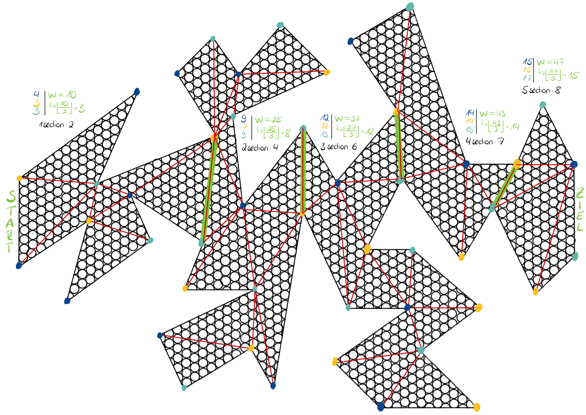

To do this, we did a triangulation per section and came up with the numbers calculated in picture 1 (coloured numbers). To make the game playable, we lowered these numbers until we found enough possibilities to hide in the museum and thus not be seen by a guard (black numbers). At the beginning of the game, there are no guards on the board. By throwing a 7 with two dice, they are put in the game. The player can place the guard anywhere. The further the pawns are on the field, the more guards are placed. If a new guard is activated, all the other guards which are already on the board also look around for that round. To finish the game, you had to reach the goal with one of your three pawns. You had to avoid being seen by a guard, otherwise you would be moved back to the green line of the section.
While playing, we noticed that it wasn´t necessary to hide because the sections were relatively narrow and you could get from one to the next quite quickly. Accordingly, the movement was always directed towards the finish. It was also very monotonous, because the only object was just to cross the playing field. We tried to counteract this with action cards, which made it a bit more fun and unpredictable, but did not change the monotony of the game. We also added secret passages in the far corners, but this did not change the fact that the best and fastest way is through the middle. Even though the art gallery problem was used quite much in this version, it had too many disadvantages and we tried to improve them.
For the second version, we started with a modular field to increase the diversity of the game. At first we created triangular fields (picture 3). However, it was difficult to find the right size and it was also difficult to fit the triangles in a complex form. Besides, there were too many fields and the whole game would take too long.

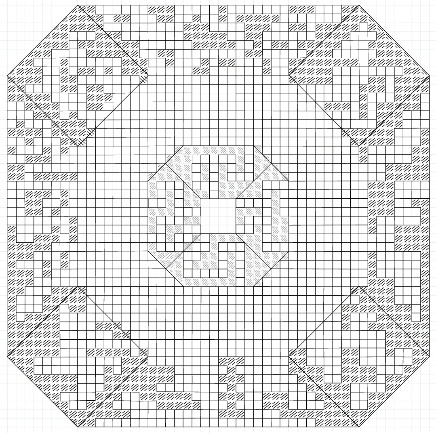
Because this version was not really playable we agreed to use quadratic fields (picture 4) and changed the goal in the game so that now we no longer have a monotonous run from start to finish. The aim of the game is now to collect treasures scattered around the playing field and bring them back to a starting field. We still had the problem that it was a little bit boring just to collect treasures, so we took up the idea with action card one more time. When we realised that action cards were rarely used, we increased the number of action card fields on our board. To see which pawn is in possession of which item we created a playing card display. One problem we already had in our first version is the difficulty in telling what exactly the guard can and cannot see. For this reason, we came up with the idea of designing our playing field in three dimensions. We added wooden cubes as walls to our playing field so that now the pawns can hide physically behind them. Because of these walls we were now able to take a laser from another game and built our own guardian block with this laser. In order to be able to use it, you have to exchange the actual guard with this block for a short time. Then you activate the laser, and you can see exactly whether a pawn is hidden behind the three-dimensional walls or whether it is hit by the laser and is thus seen and has to return to the starting point.
When we first played this version, we immediately noticed that there were too many squares on the board. For this reason, we have reduced the number. Furthermore, we have included fixed action fields and treasure fields and a line for the guards. For the guards, this means that they always walk on this fixed line and do not look around every turn, as we also had in our first version. We introduced “guard dice” and whenever a 1 is thrown, it means that the guards are activated. In addition to a six-sided dice, we also have a four-sided dice, a two-sided dice and a one-sided dice that immediately activates the guards. After each round in which the guards do not see, that is, in which no 1 is thrown, the next smaller dice is used. This means that the probability of being seen by a guard increases with each round. This encourages strategic play. In an earlier version we used a six-sided, five-sided, four-sided, three-sided, two-sided and one-sided dice. This extended the time in which no guard was activated too much, so we reduced the number of guard dice.
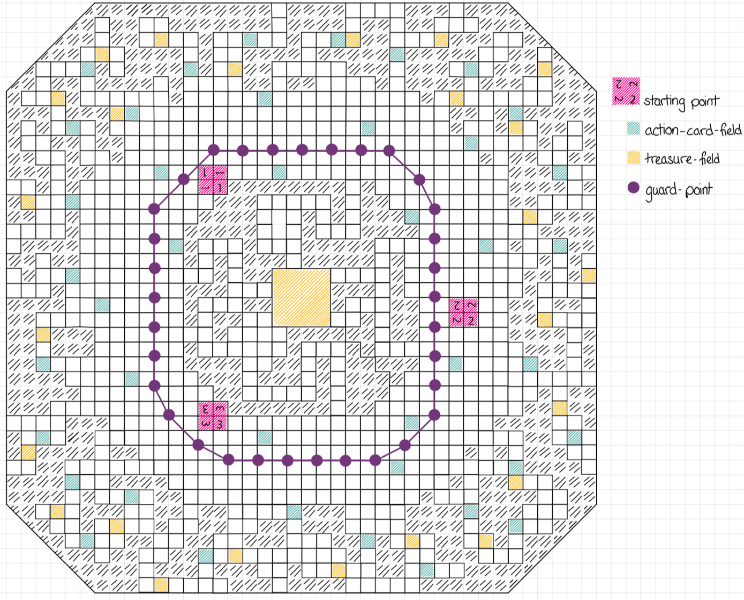
Another modification we had to make is to set the starting points closer to the inner ring, because in earlier versions they were closer to the outer modules, which made it too easy to bring back the treasures. Additionally, we used 3 dice per person and because of the 3 pawns per person it is one dice per pawn. This makes it possible to move all pawns every turn and run in different directions to collect the treasures. Besides the normal treasures on the board, we decided to place a big treasure in the middle, which has 3 times the amount of points and which ends the game as soon as it is brought back to the starting point by a player. Since there was no goal to reach like in our first version, we had determined our game end with this idea and thus made our game playable.
Through all these improvements, we have created our game ‘Museum Heist’, in which the disadvantages and problems of the previous versions are solved.
4. Our game: Museum Heist

The storyline behind our math board game is that every player is part of a group of three thieves that breaks in a museum. This museum has very labyrinthine rooms, that represent the polygons of the art gallery problem. As it is typical for burglars, the main objective of each player is to steal as many treasures as possible from the museum, which are distributed to the different rooms of the museum. There are small treasures that can be found in the halls of the museum and a big treasure (the “pharaoh’s crown”) that is worth more points and that is hidden in the middle of the playing field. Stealing the big treasure ends the game. The main difficulty linked to that is that the museum is watched by two guards. Luckily, they are not always very vigilant, so that the thieves can use those times of inattention for their heist.
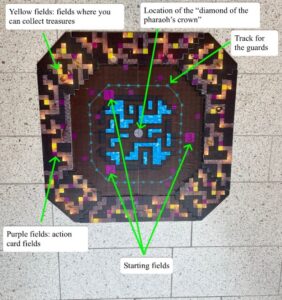
In the game this is implemented the following way: Our playing field is modular. It consists of one inner module and eight outer modules, that can be combined in different ways, so that different versions of the playing field can be constructed. In every round each player must move all his or her pawns by rolling the dice. They start their way from several starting fields in the middle of the playing field. If every player has moved their pawns, that is, when the round is over, it is decided if the two guards look around or not. For that a so-called guard dice is used. There are different types of guard dice, as already explained above. First, we use a six-sided dice. If a 1 is rolled, they look around and can see all players in their field of vision that are not hidden behind a wall.

To facilitate the decision if a pawn can be seen from the position of a guard, the game includes a laser that can be put on the field a guard is standing on and can be rotated around its own axis. If the laser hits a pawn, it is certain that the guard would see it and, in this case, it must be moved back to its starting field. If not, the pawn is safe and can continue the heist. If the guards are not activated (that is to say, if no 1 is rolled), nothing happens to the pawns. The thieves can be relieved that they have not been seen. Regardless of whether the guards are activated or not, after every round they move three fields clockwise on a colored line that indicates the path the guards are walking on, to make sure that their position always changes.
If they have not been activated in a round, in the next round a different guard dice is used. This guard dice only has four sides, which means that the probability of rolling a 1 is now increased to 25%. If they still haven’t been activated in this round, in the next round a two-sided guard dice is used, which makes a 50% probability that they will look around. If in this round still no 1 is rolled, in the next round a 1-sided dice is rolled, so that this time they will be activated for certain. Whenever the guards have been activated, in the next round we restart rolling the six-sided guard dice and in the next rounds we follow the same pattern as described above.

So in the game the player always has to show some strategical thinking: Is it better to aim directly to the treasure? Or is it better to hide behind a wall and wait one round considering the position of the guards and the use of the respective guard dice?

Another element integrated in the game are action cards. They can be collected on action card fields that are distributed on the playing field. All action cards are positive for the person that plays them, so also here strategical thinking is required, because the players have to ask themselves: Is it better to collect an action card to use it to destroy the plans of another player instead of collecting a treasure? For example, there are “handcuff”-cards which permit a player to knock-out an opponent and – if he or she is in possession of a treasure – to steal a treasure from him or her. There are also “alarm”-cards which can change the security level, that is to say, they change the type of the guard dice that will be used after this round. Other examples for action cards are “teleportation”-cards to switch the position of one of your pawns with another player’s pawn, “ventilation shaft”-cards which permit you to walk through walls, or “guard uniform”-cards which make you invisible for the guards.
Of course, there are some more action cards, but these cards and more precise information about the course of the game can be read in our rulebook, which can be found below:
5. Conclusion
With our board game you can see that math is also hidden in simple games. In the process of this project we got a fascinating glance into the world of games and have experienced first hand what it is like to develop a game idea and build your own board game. We really enjoyed our work on the board game and hope that our game and this blog post were of interest to you.
6. References
Chan, Charlotte (2010): “SETs and Anti-SETs: The Math Behind The Game of SET”, http://web.math.princeton.edu/~charchan/SET.pdf (last access: 5th of August 2023).
Chesnokov, Nicole (2018): “The Art Gallery Problem: An Overview and Extension to Chromatic Coloring and Mobile Goards”, https://math.mit.edu/~apost/courses/18.204_2018/Nicole_Chesnokov_paper.pdf (last access: 7th of August 2023).
Kaul, Hermanshu/Jo, YoungJu (n.d.): “The Art Gallery Problem”, http://www.math.iit.edu/~kaul/talks/LongArtGalleryTalk.pdf (last access: 7th of August 2023).
Mezei, Tamás Róbert (n.d.): “Extremal solutions to some art gallery and terminal-pairability problems”, https://trm.hu/pdf/phd-slides-tamas-robert-mezei.pdf (last access: 7th of August 2023).O’Rourke, Joseph (1992): “Computational Geometry Column 15”, https://dl.acm.org/doi/pdf/10.1145/130956.130957 (last access: 7th of August 2023).








