HEGL Praktika
Physics-Based Graph Layout in Hyperbolic Space
Mentor: Zachary Greenberg
Team members: David Li, Anna Roth
Description: In Euclidean space, a physics simulation has been successfully used to find graph layouts that show the symmetries of a given graph without being explicitly specified. Some graphs have hyperbolic symmetries that should be revealed via an analogous simulation on the Poincare disc. Time permitting, we can explore other geometries, including layout in 3d.
Prerequisites: Basic programming skills.
GitHub: link
Blog post: link
Video presentation: link
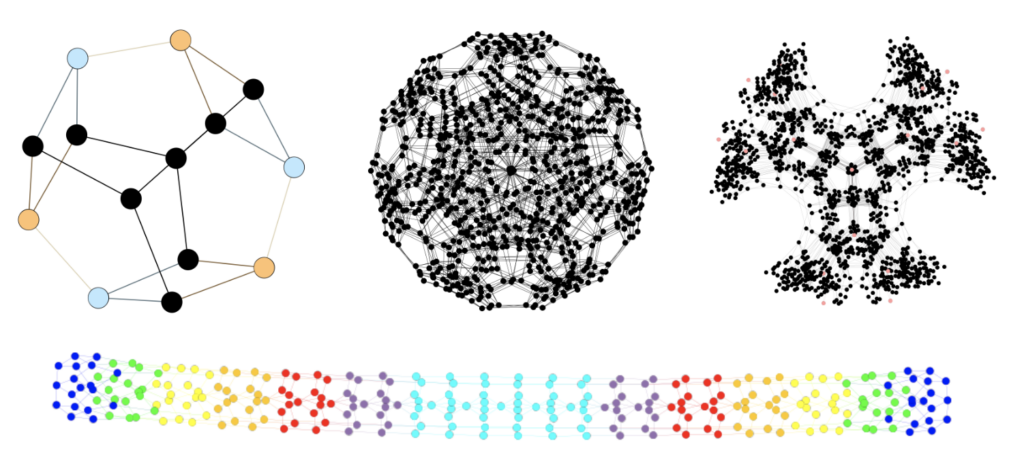
Rolling Knots
Mentors: Anja Randecker and Maurice Reichert
Team members: Leon-Josip Dzojic, Matilde Sciortino, Pirmin Kupffer
Description: In the year 1980 M. H. Freedman conjectured that every generic smooth knot in 3-dimensional euclidean space has a tritangent plane, i.e. a plane tangent to 3 distinct points. Ten years later A. M. Amilibia, J. J. N. Ballesteros and H. R. Morton used trefoil knots to construct a family of counterexamples. Such a tritangentless knot has no stable position, when sitting on a plane or table, and is therefore able to roll in at least 2 directions like a wobbly chair. A. Eget, S. K. Lucas and L. Taalman further optimized the ability to roll on Mortons family of trefoil knots by reducing the height deviation of the center of mass.
In this project our goal is to understand the proof by Morton, find new families of tritangentless knots and optimize them with respect to smooth roll-ability. Finally, we also want to 3D print these objects.
Prerequisites: Some knowledge of projective geometry, basic topology, algebra and rudimentary complex analysis skill are needed, but can be learned during the project. Basic programming skills in Python or Matlab are useful for 3D printing and Visualization.
GitHub: link
Blog post: link
Video presentation: link

Geometric Deep Learning
Mentors: Diaaeldin Taha
Team members: Sharanya Achut
Description: TBA
Math and Data Science for Social Good
Mentor: Valentina Disarlo and Diaaeldin Taha
Team members: Saifeldin Mandour, Samer Sheich Essa
Description: This project aims to leverage mathematics, data analytics, machine learning, and visualization to create meaningful insights and solutions that address problems of a social nature.
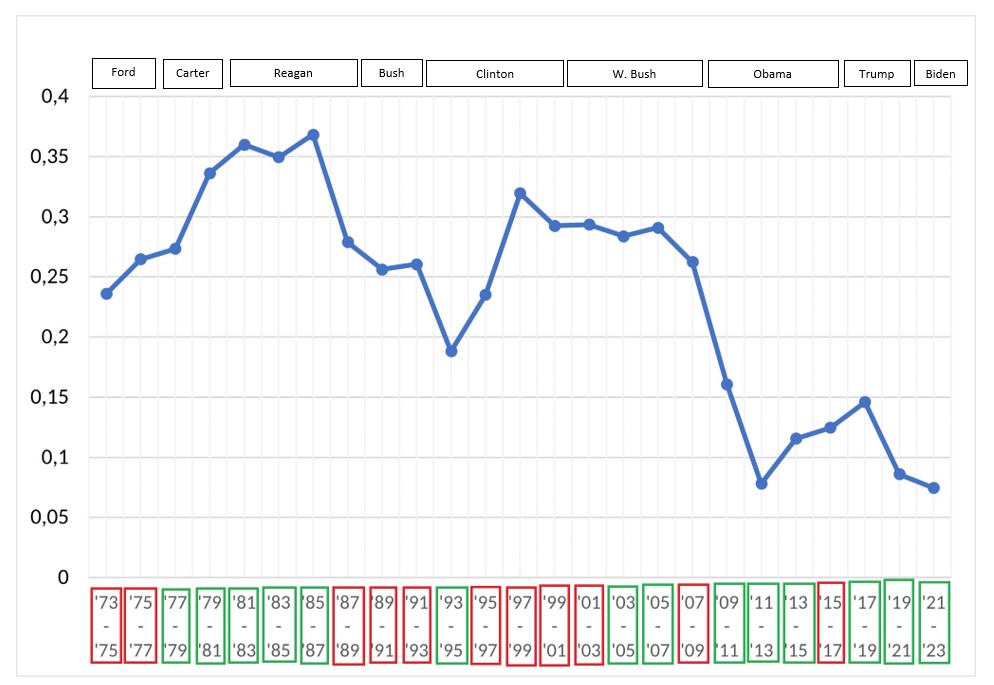
Political Geometry
Mentor: Valentina Disarlo and Diaaeldin Taha
Team members: Ayşegül Peközsoy, Leonard Späth, Klaus Stier
Description: In this project, we analyze the cross-party cooperation between US senators from 1973-2022 using co-sponsorship data. We are particularly interested in changes in cross-party cooperation over time.
Prerequisites: Some knowledge of graph theory, probability theory, and basic programming skills are needed.
GitHub: link
Blog post: link
Video presentation: link
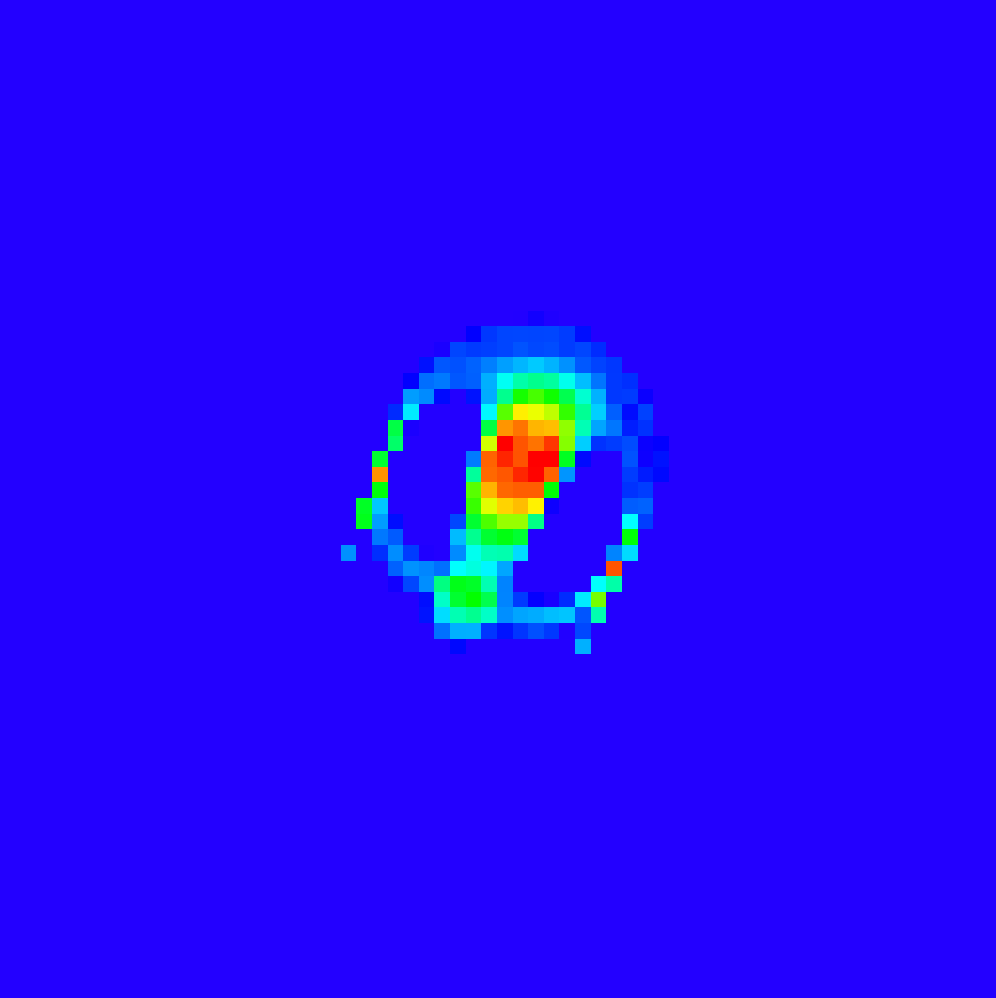
Continuous Cellular Automata
Mentor: Diaaeldin Taha
Team members: Adrian Becker
Description: Lenia is a family of cellular automata that generalize Conway’s game of life to a continuous domain. In this project, we implement two Lenia systems and optimize our implementations with mathematics and GPU programming tricks.
GitHub: link
Blog post: link
Video presentation: link

Advanced Practicals
An Interactive Web-Based Animation Application for Graph Algorithms
Mentor: Diaaeldin Taha
Team members: Tillmann Fehrenbach
Description: This project aims to build an interactive, web-based tool, ALVIS, for visualizing graph algorithms in the web browser.
Report: link
Video presentation: link

Independent Projects
Developing Outreach Materials
Mentor: Anna Schilling
Team members: Alexandra Fuchs
Description: This project aims to develop materials for math outreach and communication. The activities involved vary from organizing workshops for high school students to organizing big public events such as the Millenium Prize MathFest event from last Semester.
Aperiodic Tilings of the Hyperbolic Plane
Mentor: Anna Schilling, Diaaeldin Taha
Team members: TBA
Description: TBA



SFB Funded Projects
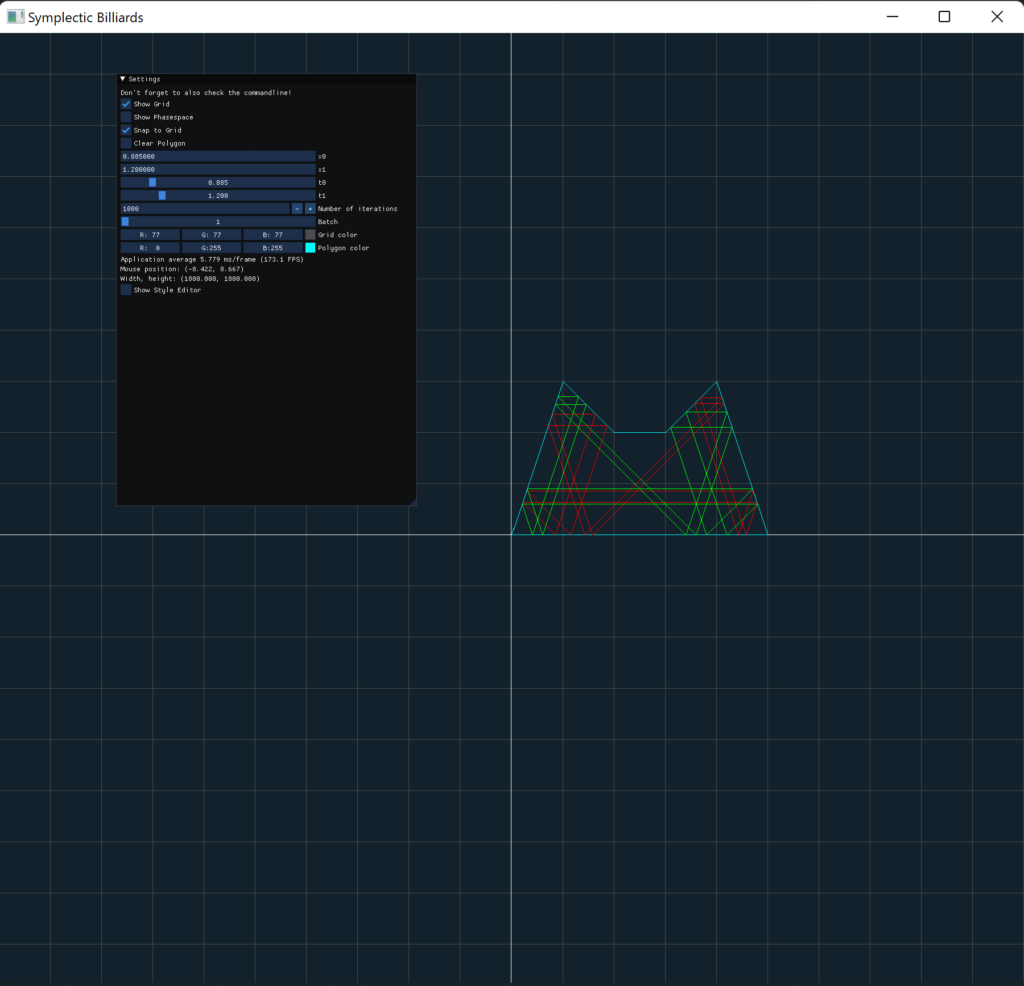
Symplectic Billiards
Mentor: Peter Albers
Team members: Fabian Lander, Jannik Westermann
Description: This project aims to simulate symplectic billiards on non-convex polygons and to search for periodic orbits in particular.
Hyperbolic Billiards
Mentor: Diaaeldin Taha
Team members: Jannis Heising
Description: In this project, we study billiard orbits in hyperbolic polygons. Using symbolic dynamics, we visualize tiles in a parameter space corresponding to triangles with particular closed orbits. We are currently refining our method for describing these orbit tiles and exploring relations with billiards in Euclidean triangles.
GitHub: link
Video presentation: link

Student Seminars Projects
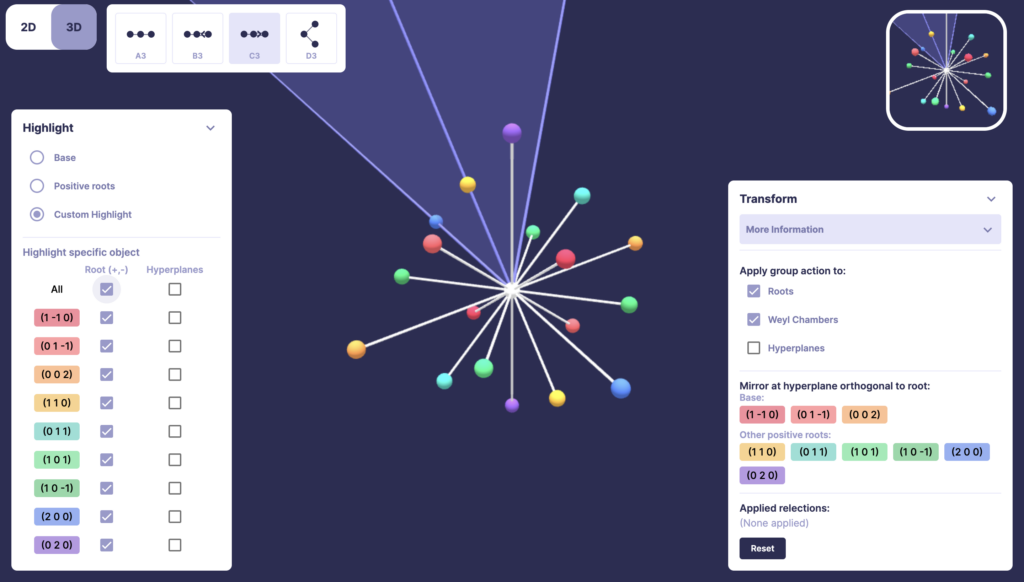
Root Systems and their Weyl Groups
Mentor: Marius Leonhardt, Diaaeldin Taha, Ricardo Waibel
Seminar: Illustrating Mathematics
Team members: Amelie Strupp
Description: This project aims to create an app for exploring root systems and their transformations in 2 and 3 dimensions and also in some higher dimensions through projections.
GitHub: link
Blog post: link
Online app: link
Quasicrystals and the Cut-and-Project Method
Mentor: Diaaeldin Taha
Seminar: Illustrating Mathematics
Team members: Noah Koopman, Ingmar Lowack
Description: In 1981, N. G. de Bruijn introduced a novel method for generating Penrose tilings by projecting particular points from a five-dimensional lattice onto the two-dimensional plane. Since then, it has been discovered that the de Bruijn method, now commonly known as the cut-and-project method, can be used to generate many families of aperiodic tilings. In this project, we will implement and optimize the cut-and-project method for some families of aperiodic tilings.
GitHub: link
Blog post: link
Online app: link
Video presentation: link

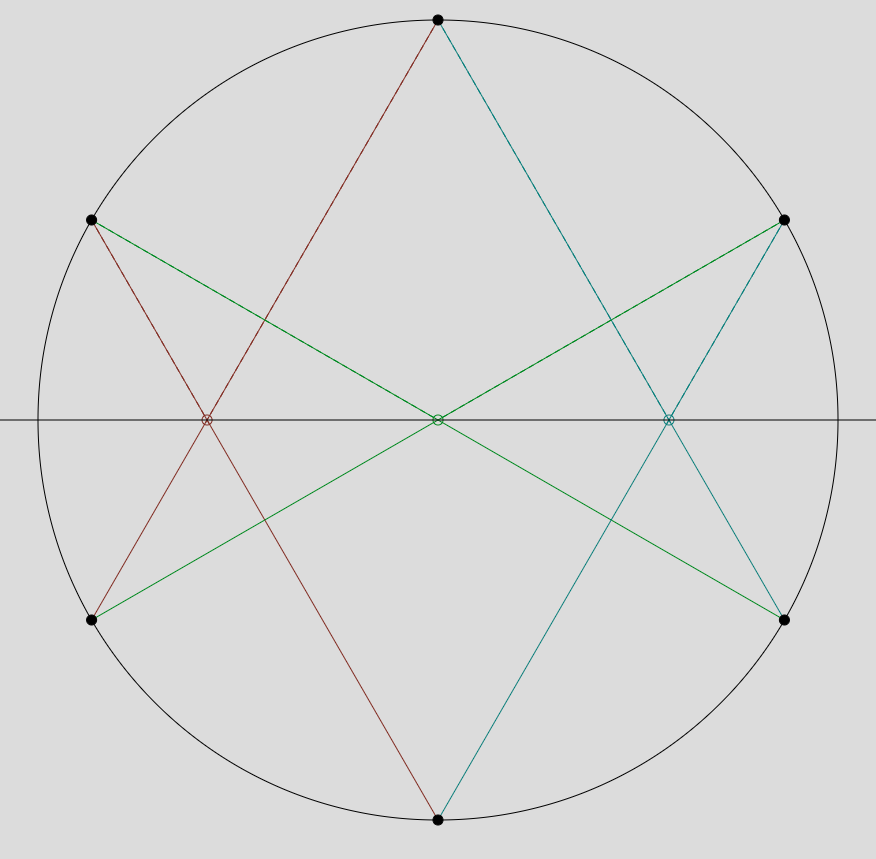
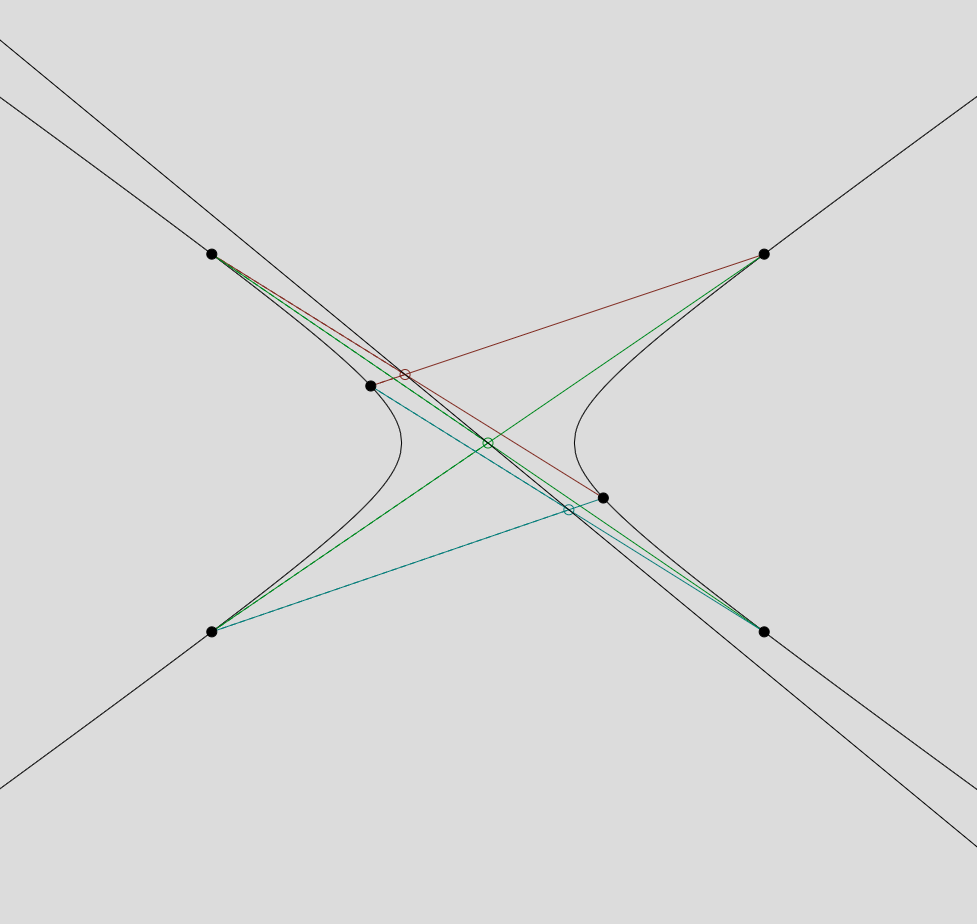
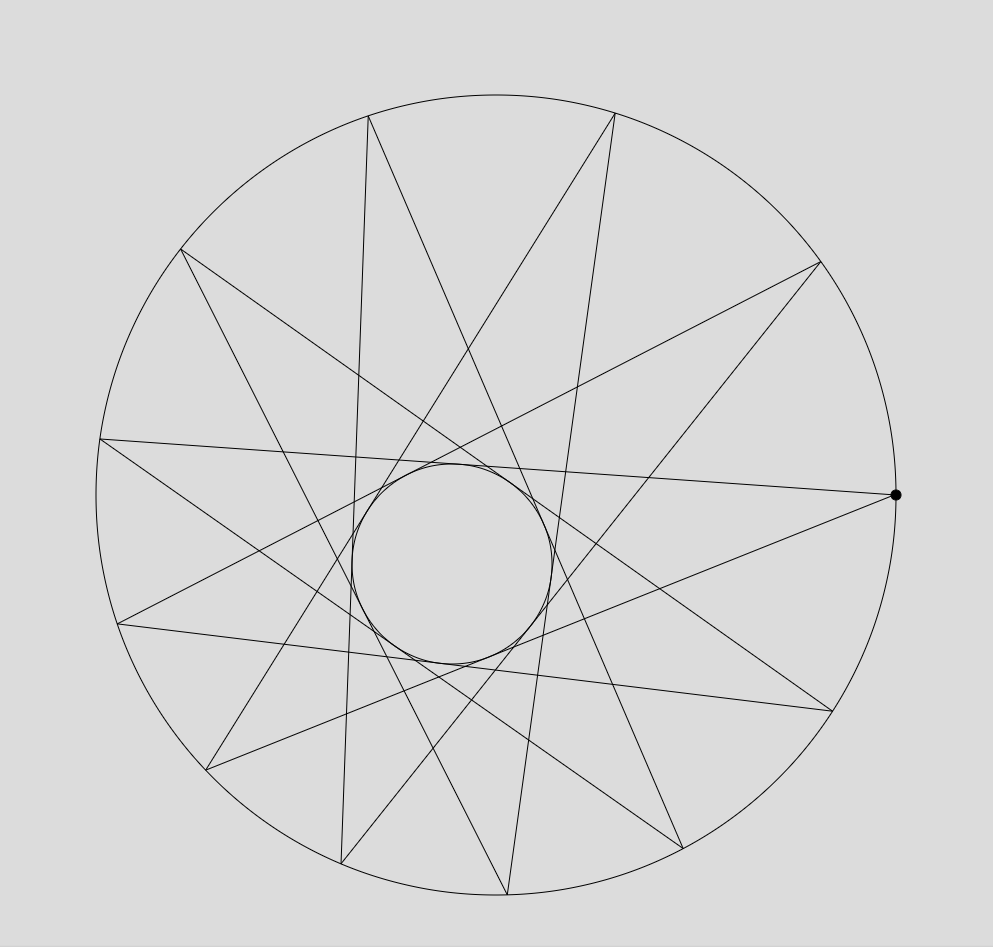
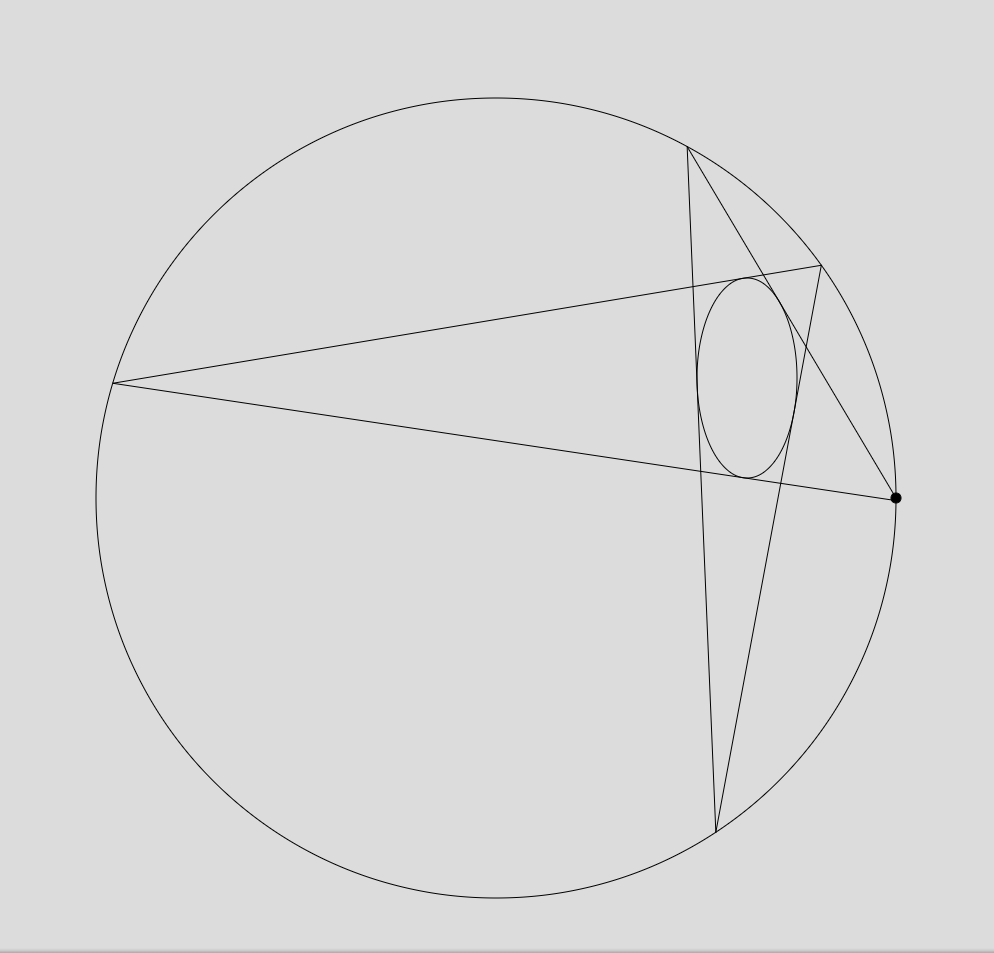
Poncelet’s Porism
Mentor: Diaaeldin Taha
Seminar: Illustrating Mathematics
Team members: Adrian Becker, Miriam Compton, Lukas Schmidt
Description: Poncelet’s porism is a deceptively simple result in geometry that states that whenever a polygon is inscribed in one conic section and circumscribes another, the polygon must be part of an infinite family of polygons that are all inscribed in and circumscribe the same two conics. [Wikipedia] In this project, we will learn the proof of the result and produce relevant visualizations.
GitHub: link (Pascal’s Theorem), link (Poncelet’s Porism)
Blog post: link
Online app: link
Video presentation: link
BOGY-Internships
Visualizing Random Walks in the Poincaré Disk
Mentors: Anna Schilling, Diaaeldin Taha
Team members: Paul Martin
Description: In this two-week internship, we will learn about the mathematics of random walks in the hyperbolic plane and simulate these dynamical systems.
GitHub: link
Online app: link

