Written by Lukas Schmidt, Miriam Compton and Adrian Becker
Introduction
During this past winter semester, we dealt with two different geometric statements: Pascal’s theorem and Poncelet’s Porism.
Pascal’s theorem
Let us consider six points \(A_1, \cdots , A_6 \in \mathbb{R}^2\) such that \(A_i \neq A_j\) if \(i \neq j\) for all \(1 \leq i,j\leq 6\) which are arranged randomly on a nondegenerative ellipse. Next we connect the six points in no particular order to form an (irregular, possibly star-shaped) hexagon. From these six lines, three pairs intersect to create three new points, defined as:
- \(Q := (A_1 \lor A_5) \cap (A_3 \lor A_2)\)
- \(R:=(A_1 \lor A_6) \cap (A_4 \lor A_3)\)
- \(S := (A_2 \lor A_6) \cap (A_5 \lor A_3)\)
\((X \lor Y)\) describes the line connecting \(X\) and \(Y\), and \(X\cap Y\) the intersection of the lines \(X\) and \(Y\). Pascal’s theorem says that the points \(Q,R,S\) are colinear, i.e., you can draw a line through the three points called Pascal’s line.
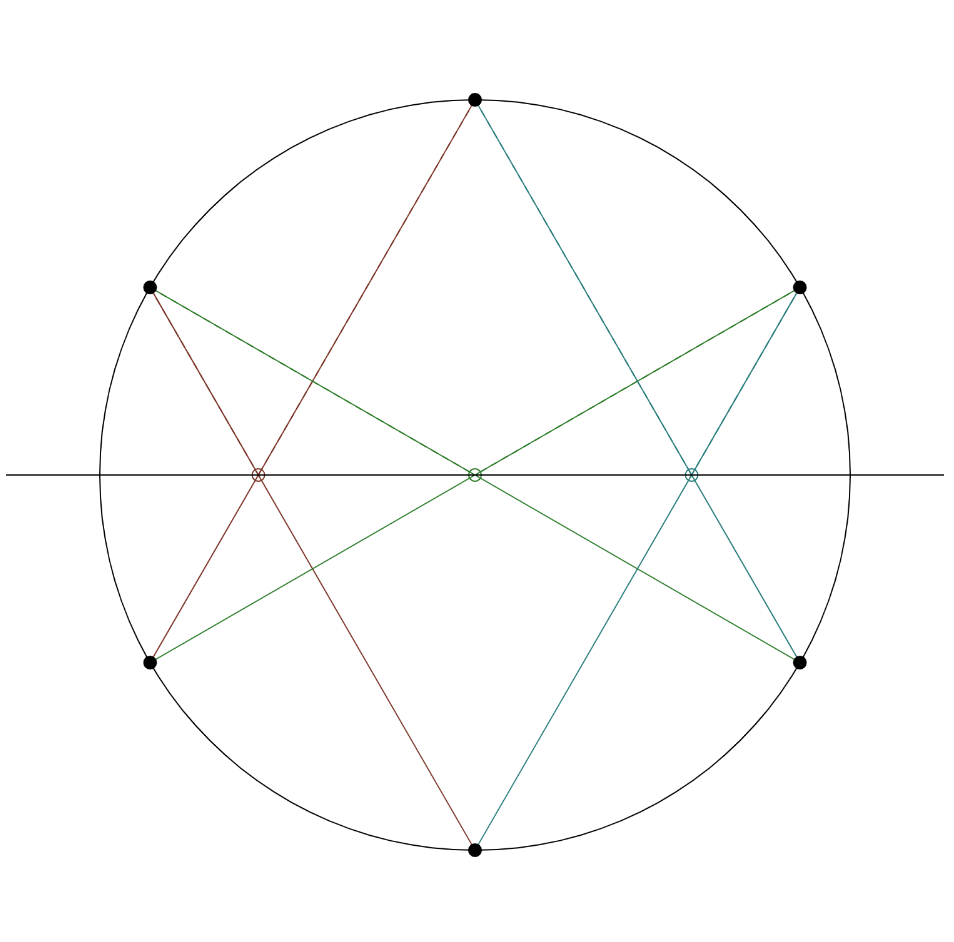
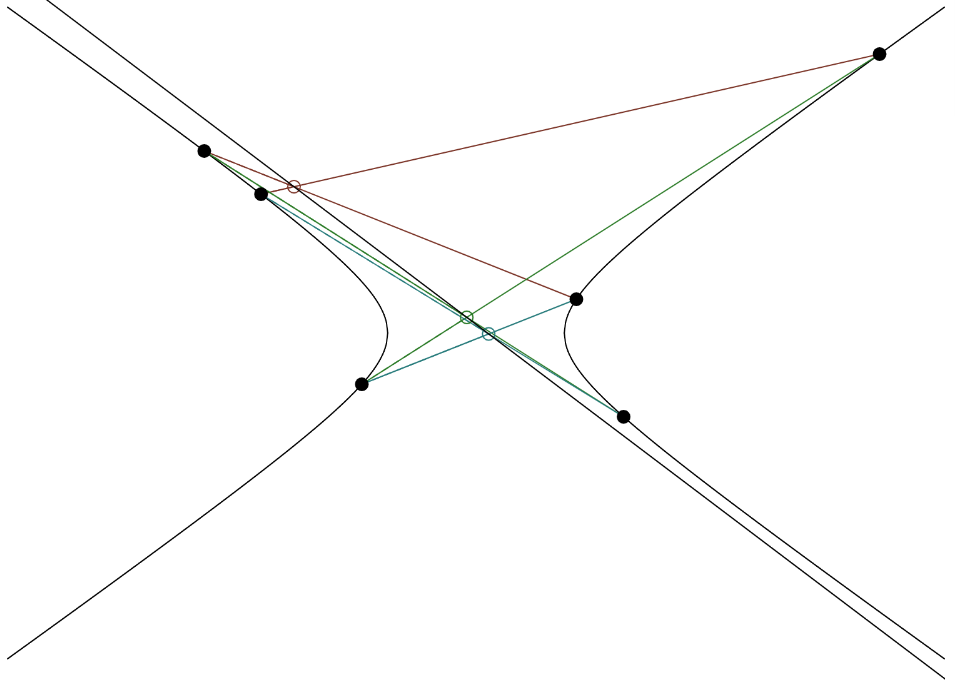
Further, Pascal’s theorem applies not only to ellipses, but can be generalized to any nondegenerate conic on which the six points can be distributed. These are
Ellipses
Hyperbolas
Parabolas
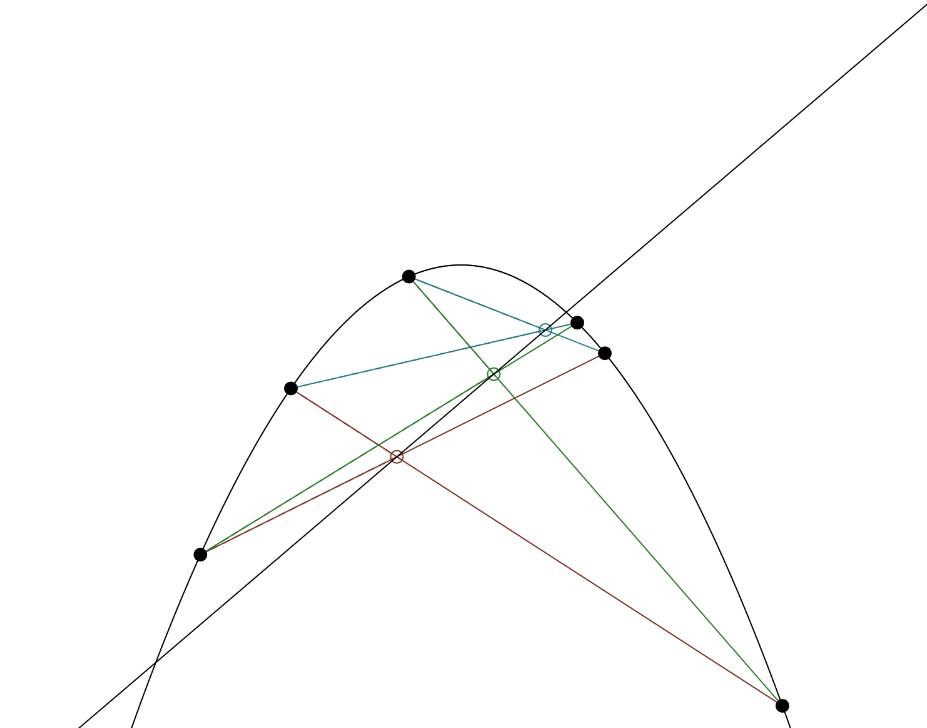
The pictures show the Pascal line on three different conics. You can find our visualization for Pascal´s theorem here.
Proof Sketch
One method of proving Pascal’s Theorem utilizes the cross ratio, which describes the relationship among four colinear points. For example, consider the line \(\overline{AB}\) with two points, \(C\) and \(D\), lying on it. Than the ratio \(\frac{|\overline{AC}|} {|\overline{CB}|} : \frac{|\overline{AD}|} {|\overline{DB}|}\) is the cross ratio of the four points. By exploiting the invariance of the cross ratio on central projections, we can proof Pascal’s theorem. A thorough proof can be found in the literature mentioned at the end of this post, so it will not be discussed further here.
Poncelets Porism
Now we will to take a look at Poncelet’s porism, another statement from projective geometry.
For this we consider two ellipses \(C\) and \(C’\), with \(C’\) completely inscribed in \(C\). Let \(P_0 \in \mathbb{R}^2\) be an abitrary point on \(C\). With \(P_0\) as a starting point, we try to construct an \(n\)-sided Polygon as follows:
- Starting at the point \(P_0\) and moving clockwise, draw a line tangent to \(C’\). Define the point \(P_1\ne P_0\) to be the point where this line meets the outer edge of \(C\).
- Using \(P_1\) as the new starting point, repeat step number 1.
You will then (potentially) obtain an \(n\)-sided polygon that circumscribes the inner ellipse and is inscribed in the outer ellipse. Poncelet’s porism states that if said polygon exists, then for every point \(P\) on \(C\), another \(n\)-sided polygon exists with \(P\) as one of its vertices. In other words, the polygon does not depend on the location of the starting point \(P_0\); it only depends on \(C\) and \(C’\).
However, it may well be possible that no such \(n\)-sided polygon exists. In which case, you would be stuck in an infinite loop repeating steps 1 and 2 above. Poncelet’s porism does not gaurantee the existance of such a polygon. It simply states that if the polygon exists, then it will always exist, regardless of the choice of \(P_0\).
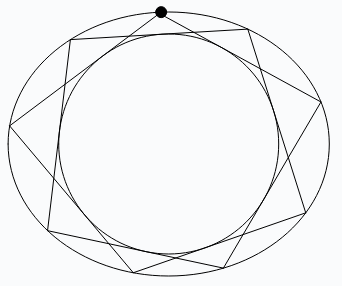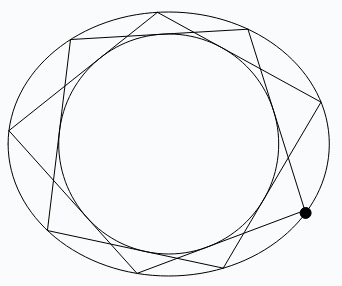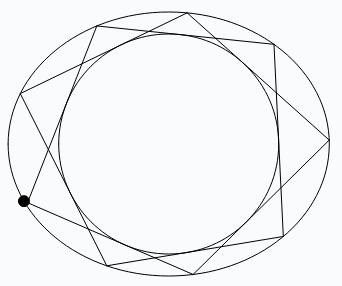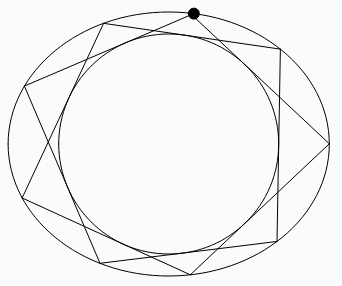
With this visualization, you can see the ellipses \(C,C’\) and the starting point \(P_0\). Starting from \(P_0\), we add an additional \(8\) points to construct a \(9\)-sided polygon. \(C,C’\) must be chosen carefully, so that we arrive back at the starting point which creates a polygon.
Cayley’s Closure Condition
Using Cayley’s closure condition we can construct curves that describe all concentric ellipses \(C\) and \(C’\) that create \(n\)-sided polygons, thus giving us useful information about when we can expect a Poncelet polygon to exist at all.
In the figure below, the green straight line represents the curve for \(n=3\). Our parameters for \(C\) and \(C’\) lie exactly on this straight line, consequently a triangle is created.
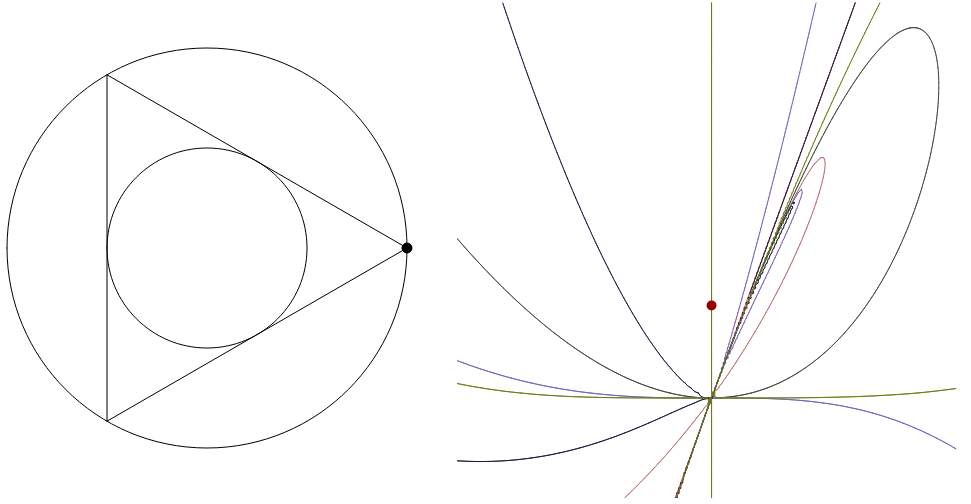
Over the course of the seminar, we wrote a program to visualize the above phenomena, with options to play around with the parameters of \(C\) and \(C’\) as well as the location of the starting point \(P_0\). You can find our visualization for Poncelets porism here.
References
Proof of Pascal’s Theorem: Kowol, Gerhard: Projektive Geometrie und Cayley—Klein Geometrien der Ebene, SpringerLink : Bücher. Basel : Birkhäuser Basel, 2009 — ISBN 978-3-7643-9902-3, S. 177
http://olivernash.org/2018/07/08/poring-over-poncelet/index.html (02.03.23)
All graphics come from our p5js program written during the 2022/2023 winter semester
