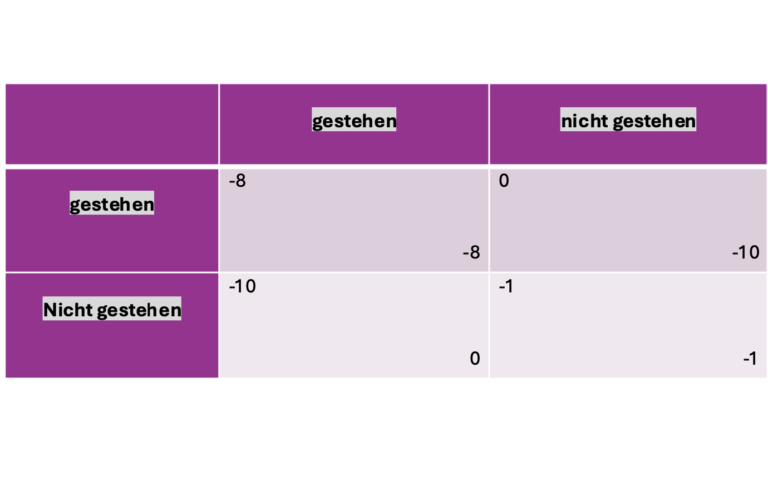
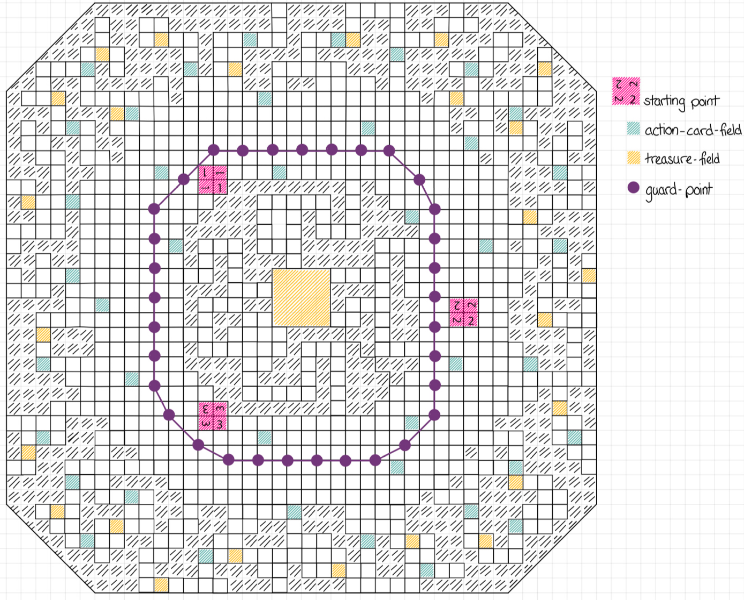
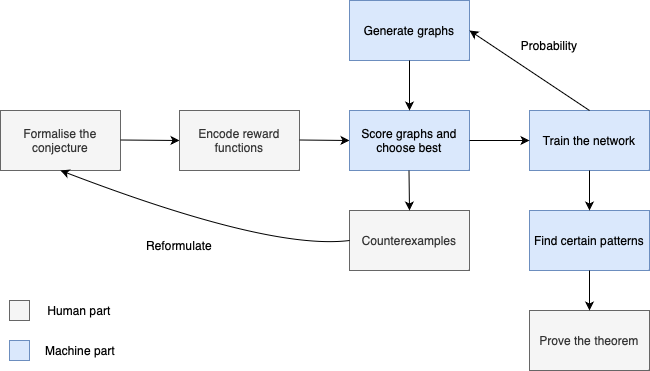
Unterrichtsvorhaben: Gerechte Teilung und die Arbeit mit Protokollen am Beispiel der Kuchenteilung
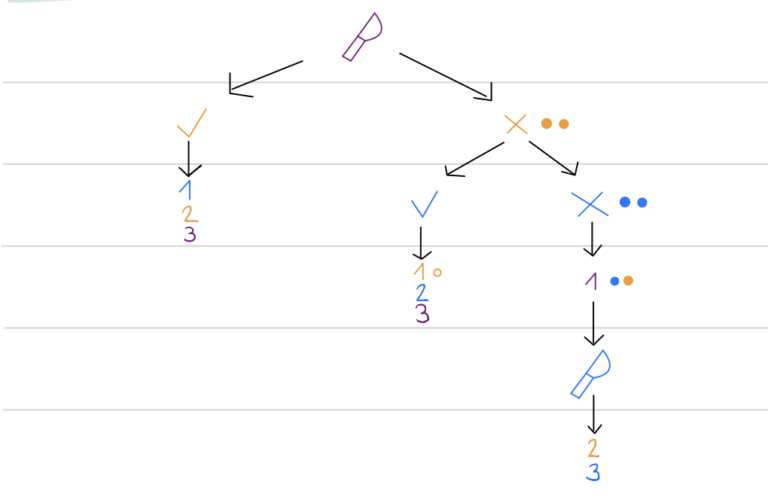
Written by Tabea Bokelmann, Malin Clasen, Eva Hettler This work was created during a HEGL seminar targeted at students in the teaching programme. As the aim is to produce materials for use in schools, the following will be in German.…