Written by Karl Schamel, Cheni Yang, and Hugo
Introduction
Many conjectures in graph theory remain open due to the hardness of giving an explicit proof, but they are also easy to be disproven by only a constructive example.
Inspired by an interesting paper on combinatorics in 2021, we have set up an environment of reinforcement learning to “attack” these problems, for example, some conjectures about the Randić index and other graph invariants.
During the game play we have encountered many issues of the framework, though our initial goal is a handy tool regarding graphs, the bigger picture of a new way of problem solving in mathematics is noteworthy.
Framework
Principle
Our model is able to find best patterns under certain constraints with the help of reinforcement learning, after more iterations the agent tends to generate graphs that will get higher scores. This is, however, not so easy for mathematicians, when they struggle to get new intuition on certain problems. More concretely, as a combination of generation and validation, some patterns of graphs will be selected and mathematicians can use them to formulate a proof or new conjectures based on the old one.
This process, described in a paper in Nature, is called “guiding human intuition with AI”. Our framework, following this way of thinking, is shown via this Flowchart:
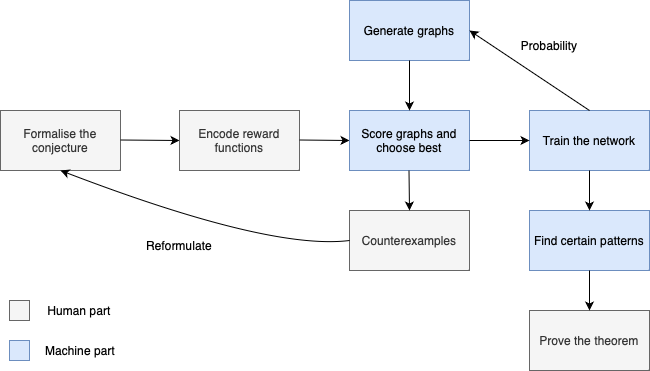
Some tools like AutoGraphiX also try to automate some parts of this process. In particular, AutoGraphiX analyzes the raw data from generation and formalizes a conjecture. However, our new powerful machine learning tools make things more universal and thus these old day tries can be rewritten in some python libraries and injected into the human-AI-human workflow.
Solving Conjectures
We show an example of settings:
Given the conjecture:
For any connected graph on \(n \ge 3\) vertices with Randić index \( Ra\) and diameter \( D\) , we have:
\( Ra\, – D \ge \sqrt{2}\, – \frac{n + 1}{2}\)
The related reward function is:
def conjecture2(actions):
graph = nx.Graph(actions_to_adj(actions))
if not nx.is_connected(graph):
return 0
D = nx.diameter(graph)
return 10-(Randic_index(actions_to_adj(actions))-D- np.sqrt(2)+ (N+1)/2)We have partially checked some conjectures from Chemical Graph Theory, especially on the Randić index, and come to the conclusion that in small sizes (\( n \le 20 \)) the graph generation indeed converges to optimal patterns mentioned in the paper. Although we failed to find a counterexample due to the limitation of computational ability, we surely have worked out a robust solution to embed these conjectures into the scheme of machine learning.
A small but interesting application of this model may be in the sudoku game, which is equivalent to some certain graph coloring problems. The model succeeds in going into the proper direction of solutions with the proper action encoding and loss function. That is to say, given a blank board, the model will try to find a suitable coloring to match all constraints of the problem, and if a suitable encoding of a game is provided, the agent will also adjust itself to learn from these initial states and output a correct answer.
We have also dived into the combinatorial problems in the original paper and discovered similar results, almost all converge actually very quickly to the mentioned patterns (some to local extrema though), which is a good support of the correctness.
Issues
One problem we encountered with our model was the convergence to local minima. In this chapter we will delve into this issue.
The Problem of Convergence
The problem of convergence arises when the ML model, specifically a neural network in this context, learns from the best-generated graphs repeatedly. In many cases, these generated graphs share the same or very similar structures. Consequently, when the learning process is iterated multiple times, the model tends to converge to local minima, getting stuck in a specific solution instead of exploring the broader solution space.
Solution 1: Novelty-Search
In the context of novelty search, the model prioritizes the generation of diverse and novel solutions over solely focusing on the best-performing graphs. The model is encouraged to explore different avenues and embrace novel structures that might lead to better outcomes.
To achieve this, a factor is introduced into the reward function that measures the distance or dissimilarity of the generated graphs from the already found optimum.
However, the main difficulty lies in finding an appropriate similarity measure. Firstly, what does similarity of graphs mean? And secondly, this measure should strike a balance between being general enough to cover a wide range of graph structures and being specific enough to capture relevant information related to the conjecture being addressed.
The best choice would be a graph isomorphism measure. Unfortunately, these isomorphisms are too computationally expensive making this measure infeasible.
We tried a linear combination of common graph metrics like girth, diameter and maximum/minimum degree together with a conjecture specific factor. Choosing these constants wasn’t clear and was usually a trial-and-error process. If not configured correctly either a complete or an empty graph were learned.
The following code defines a similarity measure:
def reward(A, currentBest):
"""" A is given as an np adjacency matrix
Returns reward for given Matrix A
"""
return globals()[f"reward_c{conjecture_number}"](A) + 0.132 * similarity(A, currentBest)The major issue with this entire approach of adding a novelty score to the score of the conjecture is the trade-off. It is not at all clear how to choose it, because depending on the constants of the linear combination, we either had too much weighting of the similarity measure or the conjecture score. This led to the convergence to a completely irrelevant extremum of the adjusted reward or an unchanged convergence.
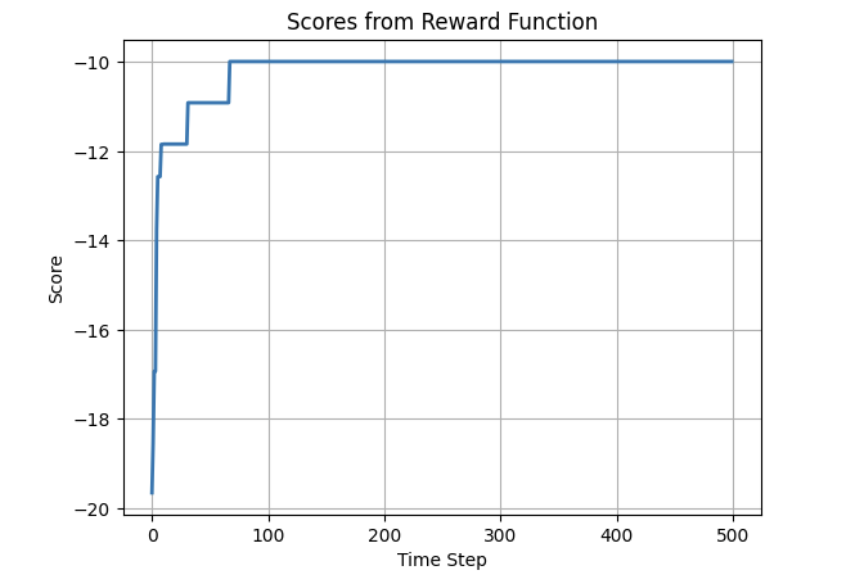
Next Steps:
- Add novelty iterations which add some local divergence from the current path every couple of iterations.
- Add dissimilarity measure only with respect to the already found optimum. Choose as an indicator function for similar but not identical solutions and as a continuous function for generally different solutions. What has yet to be found is how this continuous function should be selected, such that the local optima so the reward function remains unchanged.
Solution 2: Clustering
Clustering is another powerful technique to tackle the convergence problem. The idea behind clustering is to train multiple agents on different seeds (random initializations) and allow them to learn independently. Each agent explores a unique portion of the solution space, which often results in diverse performance levels among them.
Procedure:
- Initial generation of 500 graphs
- Partition into 5 clusters
- Train one agents per cluster for 30 iterations
- Train each agent independently
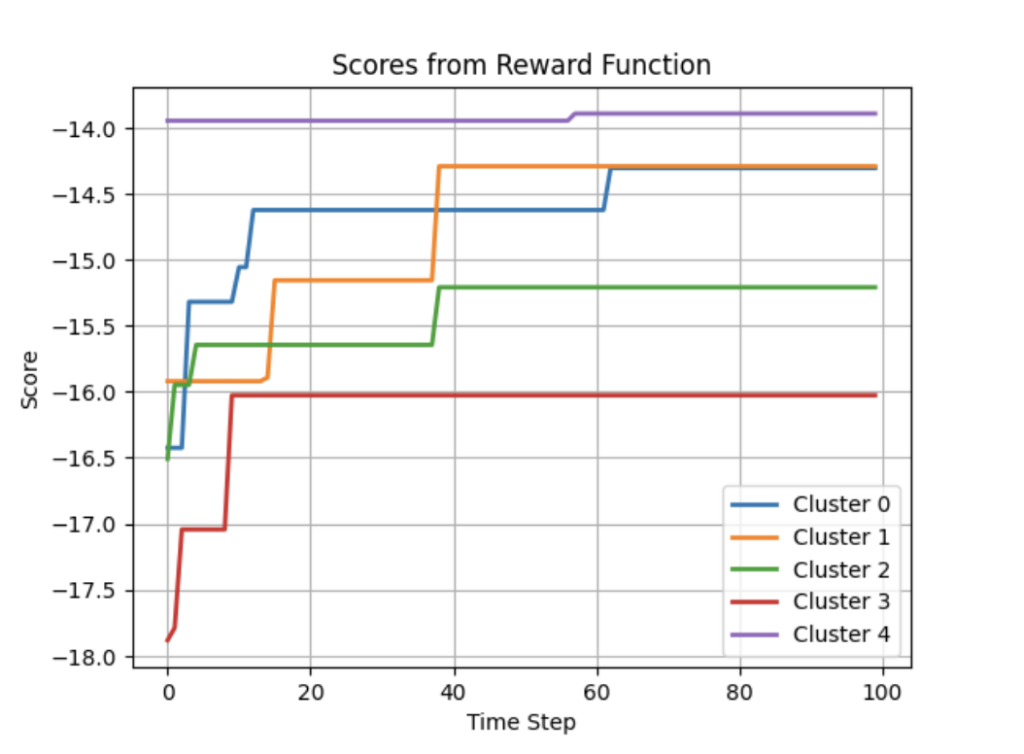
With this approach we have a different starting position for each agent, which means that each agent is more likely to generate a graph similar to the ones in the cluster it is based on. This “likeliness” depends on the number of iterations the agent has been trained on.
Results:
As apparent in Figure 2, the different agents often converge to the same local optima, but there is often only one or a few agents which converge to the best graph. Oftentimes this will eventually be achieved by the other agents. However, this might take considerably more time.
Thus, we think that clustering could help speed up the learning process.
Next Steps:
- Add clustering iterations where many graphs are generated with the current agent, and we do the clustering framework.
- Use clustering networks which train multiple agents in parallel and then do another clustering step with only the best agent so it won’t become exponential.
- Use clustering to identify promising structures which are not on the path to the current optimum.
The Computational Bottleneck
Being a reinforcement learning algorithm, it it crucial to generate a vast number of graphs each iteration to ensure enough good results to learn from. Successful use of the algorithm results being very computationally expensive and might, on personal computers, require several hours to approach a result.
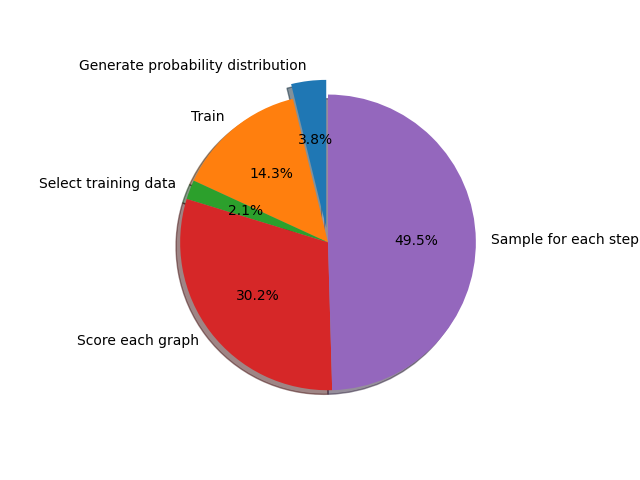
In Figure 3 we see the shares of the total runtime the respective parts of the program claim for one iteration. Here, the algorithm was used to generate 5000 graphs with 17 nodes per iteration, which is a realistic setup for many different problems. The graphs are then scored based on a combination of diameter and Randić index.
As can be seen, the computational bottleneck is not the training of the net, but surprisingly the generation of graphs and their subsequent scoring. While the complexity of the sampling part of the algorithm depends solely on the graph sizes and number of graphs per iteration, the computational complexity of the scoring function might vary strongly when comparing the different theorems one can approach with this method. Sometimes, acceleration of this part is not possible due to lack of quick calculation methods for special constants. For Figure 3 a score function of roughly intermediate runtime among problems of chemical graph theory was chosen. The slow speed of roughly 30% of the runtime results from the need to score each graph individually.
The time it takes to sample out the probability distribution given by the neural network however amounts to roughly half of each iteration, as every graph has to be sampled out independently and step by step. Speedups can be attained for example by Just-In-Time compilation with Numba. The sampling task is also highly parallelizable and optimal for GPU computation, whereas Figure 3 shows the runtime of a fully sequential calculation.
It should be noted that the generation of the probability distribution as well as the sampling scale linearly with both graph size and number of graphs per iteration, whereas the other parts show a quadratic behavior or higher.
Conclusion
We have considered the general setting of solving conjectures on graphs. Under the initial goal we developed a reinforcement learning model and analyzed issues that cause the wrong output or make the program under the performance.
We hope this report can give readers some impressions on how neural networks can empower the symbolic AI and help mathematicians skip some annoying trivial jobs, as well as obtain solutions in a way that would otherwise go against human intuition.
