Written by: Caroline Bornmann, Sebastian Grafe, Johannes Kamlage
The reason why Heidelberg is better than Granada

Granada in Spain. Roughly 230.000 habitants and a beloved holiday destination for many tourists. But why exactly is this beautiful piece of land in Andalusia such a big deal for mathematicians which still leaves remaining questions? And last but not least, why do we claim that Heidelberg is even better than Granada?
This last semester, we were part of the HEGL Seminar: Illustrating Mathematics (Groups and Symmetries). Before we can answer the questions from above, we need to explain some basic knowledge regarding our work with symmetric groups, isometries of the Euclidean plane as well as wallpaper groups.
First of All, Some Definitions
The Euclidean Plane is a Space of Dimension 2, where two real numbers define the position of each point. For example, the \(\mathbb{R}^2\) we all know from school works as an Euclidean plane. What is quite important for the further steps in our presentation until we reach wallpaper groups in general is the fact that all the isometries of the plane form a group under composition of functions, the so called \(\mathbb{E}^2\). This can easily be proven directly. Now for the isometries: Imagine any kind of pattern. You almost always have some kind of isometries somewhere in these patterns. For example, a so-called translation. That is a part in the pattern which can be shifted in any direction, so that the pattern still looks the same. This is actually really cool about wallpaper groups, as even though they are categorized via lattices (which will be further explained later in the text) you could technically do a translation in any given direction due to the fact that the pattern of the wallpaper group is never ending. But generally, if you talk about wallpaper groups you only consider the two translations which are responsible for the lattice type. In the Euclidean plane, we could define a function \(f(x) = x + r\), which translates every point \(x\) to the new point \(x + r\), so we have a translation by \(r\). The mathematical correct term would be that the pattern stays invariant under translation as we do not want to transform the whole plane but for getting the grasp of our project thinking of a translation is good enough. Then there are reflections. We imagine an axis where we can hold a mirror next to a part of our pattern and the reflection in the mirror is exactly identical to the part of the pattern behind our axis. The most common axes in the Euclidean plane are the \(x\)– and \(y\)-axis. So, by defining the function \(g(x, y) = (x, -y)\) we can mirror all our points \(x\) from above the \(x\)-axis below it and vice-versa. If we combine these two isometries together by starting with a reflection and then translate parallelly to the line of reflection, we get another isometry. This is called a glide reflection and will help us further categorize our wallpaper groups. Now the only isometries that are left are rotations, which are self-explanatory. Especially helpful here are the so called rotation matrices using sine and cosine. If you are further interested in the Euclidean group and its isometries, we can recommend Chapter 24 of the book “Groups and Symmetry” by M.A. Armstrong, which goes into more detail on the group \(\mathbb{E}^2\).
In some patterns, we encounter several kinds of \(n\)-gons (polygons with \(n\) vertices). After numbering the vertices from \(1 \ldots n\), a rotation or reflection of the \(n\)-gon now corresponds to a permutation on the first \(n\) integers. A permutation is a bijection \(f: X \rightarrow X\) for any set \(X\). Considering the \(n\) vertices, we set \(X = {1, \ldots, n}\). Often one can already see in the graphical sense that the rotations and reflections form a group. If those rotations and reflections are considered as permutations on \(X = {1, \ldots, n}\), it is not surprising that there is an isomorphism between the group in the graphical sense and \(S_X = S_n\). (\(S_n\) is the symmetric group containing all permutations on \(X = {1, \ldots, n}\)). But there is a stronger theorem, namely Cayley’s Theorem which states that any arbitrary group \(G\) is isomorphic to a supgroup of \(S_G\). Now with this basic knowledge about isometries, we can talk about wallpaper groups.
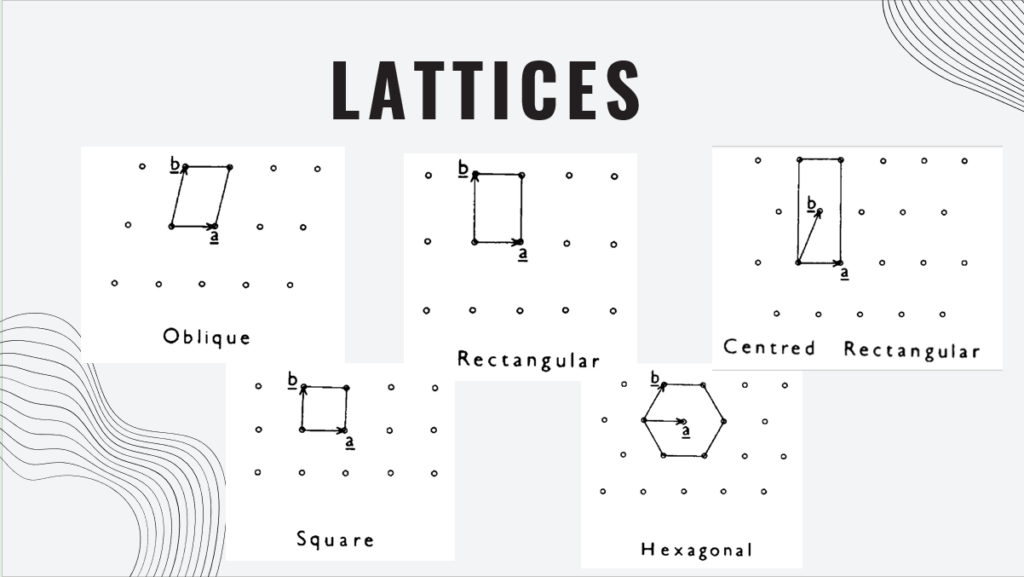
A wallpaper is an object in the Euclidean plane, a two-dimensional repeating pattern, that covers the plane through the repetition of certain isometries which keep the patterns unchanged. Wallpaper groups classify these repeating patterns into different groups based on their symmetries. To formally define a wallpaper group, it can be understood as a group of isometries of the plane that contains two linearly independent translations and rotations of angles 180°, 120°, 90°, or 60° only. In order to talk about wallpaper groups in more detail, the underlying structures need to be taken into account. The significance of this structure – a so-called “lattice” – in the context of wallpaper groups lies in its role as the grid generated by the two translations, providing the framework for the repetition of the pattern. Specifically, a lattice is a set of points in the plane such that, when translated by the lattice vectors, the pattern exactly repeats itself. There are five distinct types of lattices that are of importance in this context: the oblique, rectangular, centred rectangular, square, and the hexagonal lattice. There are two oblique wallpaper groups, five rectangular ones, two centred rectangular ones, three wallpaper groups on square lattices and five on hexagonal lattices. This means that the total number of wallpaper groups comes to 17. To get the full mathematical proof for that, you can read Chapter 25 of “Groups and Symmetry”. To now answer the first question from the beginning, this is actually the reason for the dispute of some mathematicians. There are a few that believe that in Granada, especially in Alhambra – a fortress complex in Andalusia – all 17 wallpaper groups are present, but some other mathematicians think otherwise. With our project, we wanted to show that we can do better with our new knowledge about wallpaper groups and give some people another reason why they should come and visit Heidelberg and especially the Mathematikon, as we can guarantee that all 17 wallpaper groups are contained here. To prove this, we will now present pictures of 3D-Models, Structures, and typical objects which can all be found in the Mathematikon.
Explanation for Classification
Different operations will be denoted by different symbols or numbers, so from now on, we will denote “p” for primitive structures (structures where the basic parallelogram does not contain lattice points in their interior) and “c” for centred structures which do so. A reflection will be denoted with “m” for mirror and a glide reflection with “g”. The numbers 2, 3, 4 and 6 will indicate the order of rotation (e.g. “2” would be a half-turn).
For example, if we look at the group p4gm, it has two centres of rotation of order four (90°),
which are each other’s mirror image, but it has reflections in only two directions, which are
perpendicular. There are rotations of order two (180°) whose centres are located at the
intersections of reflection axes. It has glide reflections axes parallel to the reflection axes, in between them, and at an angle of 45° with these.


Pictures for all the other wallpaper groups in Heidelberg can be found in our Powerpoint. We hope we could inspire you to come visit us, as clearly, Heidelberg is better than Granada.
