Written by: Bastian Hirschfeld, Heidi Rhodes James, Arjan Siddhpura, Ioana Todosi
In the past semester we have developed a website that shows computer generated compositions in the style of Victory Boogie Woogie which is Mondrian’s last and unfinished work.

To teach a computer how to replicate VBW one must first understand what it entails and to our surprise that a lot of the details in this painting contain recycled elements from previous work, even though this previous work doesn’t look like anything of the Mondrian’s that we know of today. Some of these elements are:
- bright primary colours first appear in his impressionist painting


- his cubism paintings progress show his affinity for creating order in chaos



- when he established the De Stijl movement, his compositions were simple, but each of them combined create VBW:
- the lines from these iconic paintings,
- the checkerboard here is also present in VBW

- the painting closely mimics BBW, with the yellow lines and the overall composition

Each of these elements give rhythm and harmony to the chaos that we perceive at a first glance. In its essence VBW is meant to represent the vibrant lifestyle of New York
Our program is based on Prof. Loe MG Feijs’ article “A program for Victory Boogie Woogie” which showcases a successful attempt of imitating VBW algorithmically. Prof Feijs tried multiple approaches to build these compositions (using regular grids and perturbing them, recursively splitting the plane and its subplanes, drawing random triangles) but none of these approaches came close to replicating the essence of VBW.
The final implementation consists of letting lines and planes compete for space on the canvas.
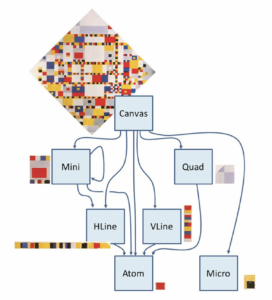
The building block of our whole project is a single class called the Cell. All other objects are mutations of this cell object. The cell regulates its own growth and also takes care of how to interact with its neighbours, its children and its own parents, rendering itself finally on the screen. The root of this recursive tree is called the Canvas, where it all begins by setting up various types of cells. These include the horizontal and vertical lines that begin drawing first, Quad objects having four cells within themselves to create the borders of the Canvas, a Micro object that has a recursive nesting of one level, ie it has a cell within itself and lastly, Mini which makes use of fuzzy logic to determine the type and number of cells that are created within itself recursively. The simplest manifestation of the cell is called the Atom, which forms the leaf of our recursive tree by being a simple square. All of these cells are also simultaneously coloured in the palette of the Victory Boogie Woogie Painting by Piet Mondrian.
We make use of various technologies like HTML, CSS, JavaScript and combine it with P5js to render this website.
The style of implementing the painting with the composite pattern leads not to just a single copy of the Victory Boogie Woogie, but to a wide range of similar canvases. Some of them are much better than others, but all of them include the characteristic “Mondrian Style”.
Even though there are challenges to solve and improvements to make. For example, relative sizes of the patterns for a better experience with bigger screens or mobile phones. More buttons can also be an idea to improve the user experience by slowing down the animation, speeding it up, or even changing the colour palette.
As Victory Boogie Woogie was unfinished when Mondrian died, there is much space for interpretation.
Our website is like the real Victory Boogie Woogie work in progress and as Mondrian removed parts of his painting and added new ones, always trying to improve the result, our work can be described similarly.
Our final project can be found here: https://hegl-lab.github.io/Seminar-SS23-Boogie-Woogie/ and the code is available on GitHub: https://github.com/hegl-lab/Seminar-SS23-Boogie-Woogie
Resources:
- “A program for Victory Boogie Woogie”, Loe MG Feijs, https://doi.org/10.1080/17513472.2018.1555687
