Root Systems and their Weyl Groups

Written by Amelie Strupp

Introduction

This project aimed at providing an interactive application to visualize Root Systems and their
corresponding Weyl groups.

The final version is available through the following link.

Prerequisites

This section introduces some important concepts by using visualizations generated by the application. We begin by defining the concept of a Root System:

Definition 1 (Root System [1, p. 184]). Let \(E\) be a a finite-dimensional Euclidean vector space with the standard Euclidean inner product. A Root System \(\Phi\) in \(E\) is a finite set of non-zero vectors (called roots) that satisfy the following conditions:

1. The roots span \(E\)
2. The only scalar multiples of a root \(\alpha \in \Phi\) that belong to \(\Phi\) are \(\alpha\) and \(-\alpha\)
3. For every root \(\alpha \in \Phi\), the set \(\Phi\) is closed under reflection through the hyperplane perpendicular to \(\alpha\)
4. Integrality: If \(\alpha\) and \(\beta\) are roots in \(\Phi\), then the projection of \(\beta\) onto the line through \(\alpha\) is an integer or half-integer multiple of \(\alpha\)

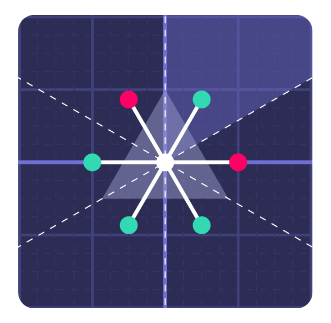
While there are infinitely many root systems, they can be classified through the different types of connected Dynkin Diagrams. More precisely: there is a 1:1 correspondence between those diagrams and the indecomposable Root Systems up to isomorphism. [2, p. 6]

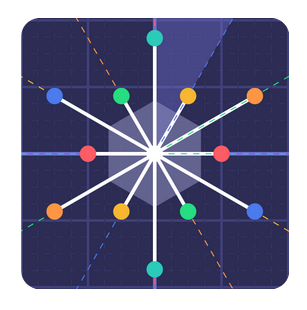
Two other concepts related to Root Systems are Weyl Chambers and Weyl Groups:

Definition 2 (Weyl Chambers [1, p. 210]). The complement of the set of hyperplanes orthogonal to the roots is disconnected. The individual components are called Weyl Chambers.

Definition 3 (Weyl Groups [1, p. 198]). The group of isometries of the Euclidean vector space \(E\) generated by reflections on hyperplanes orthogonal to the roots is called the Weyl Group of the root system.

Our Visualization

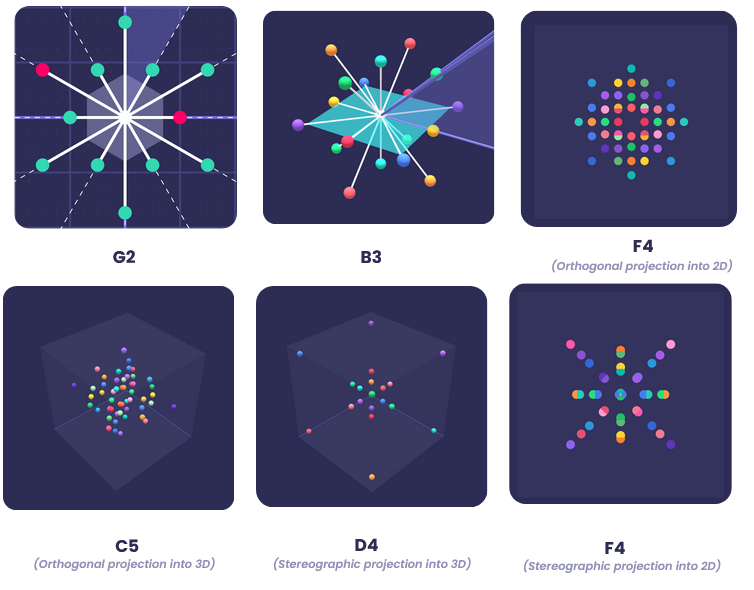
We visualized the different possible Root Systems in up to 6 dimensions. To display objects of higher dimensionality, we employed stereographic and orthogonal projections.

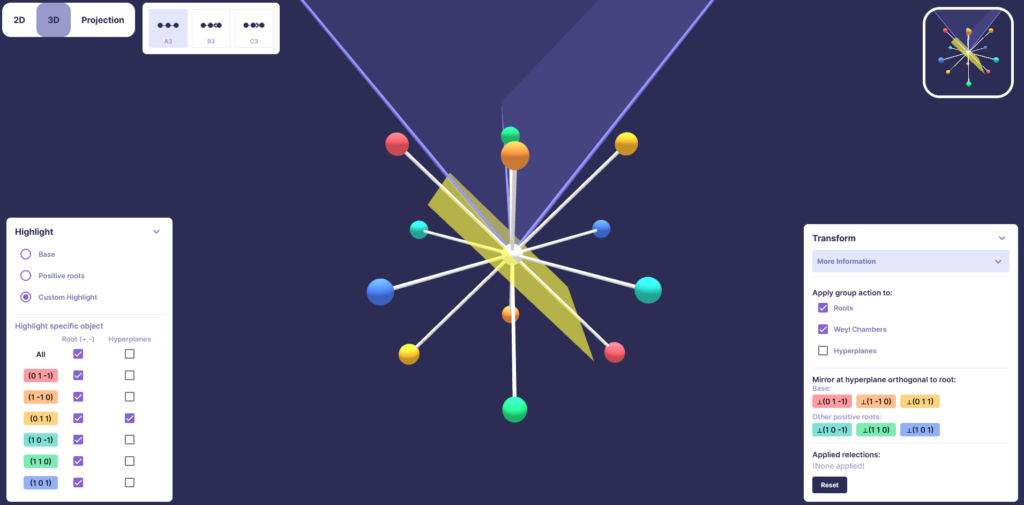
The web application allows users to visualize the action of the Weyl Group on the Roots. Moreover, certain properties like a possible choice for base vectors and the corresponding positive roots can be displayed. For the two-dimensional case, it is furthermore possible to also inspect the integral weights.

For dimension 4 and above there are two different types of projections available: Stereographic or orthogonal projection. Furthermore, it is possible to adjust the rotation of the root system or the corresponding projection plane. Information about the current rotation is available on the bottom-right part of the screen.

References:

1. Brian C. Hall. Lie Groups, Lie Algebras, and their Representation. Springer Cham, 2016. isbn: 978-3-319-37433-8.
2. David Mehrle. Root Systems and Dynkin Diagrams. URL: http://pi.math.cornell.edu/~dmehrle/notes/old/promys14/rootsystems.pdf (visited on 03/06/2023).