Visualizing the Hopf fibration

Written by Jonas Höcht, Burak Ertan und Carola Behr

The famous physicist Sir Roger Penrose called the Hopf fibration “an element of the architecture of our world” – reason enough to try and visualize this remarkable map.

Through the formalism of quaternions, \(S^3\) (the sphere in four dimensions) can be identified with the set of rotations of \(S^2\) (the spere in three dimensions). The Hopf fibration now maps a point \(r\) from the \(S^3\) to the point \(P\) on the \(S^2\), to which the point \((1,0,0)\) gets rotatated by the rotation defined by \(r\).

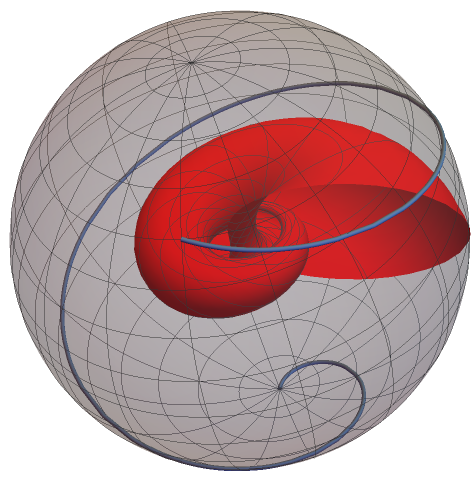
It turns out that in this construction, the preimage of a point \(P\) on \(S^2\), called the fiber of \(P\) under the Hopf map, is a circle on \(S^3\). Being humans, we unfortunately cannot see the structure emerging from this in 4 dimensions. But instead, we can use stereographic projection to construct a visible image of the Hopf fibers. As different circular fibres on \(S^3\) are interlinked and stay interlinked circles in \(\mathbb R^3\) under projection, beautiful structures emerge by looking at the Hopf fibrations of curves on the sphere.

The figures show different visualisations of the Hopf fibration of a spiral on the sphere.