Written by Deniz Aydın and Simon Heidrich.
It is easy to imagine how spherical triangles are “fatter” than Euclidean ones. Just like this, hyperbolic triangles look slimmer in comparison. Gromov used this property to generalize hyperbolic spaces. Imagine δ-neighborhoods of the sides of a triangle. If every edge of a triangle is covered by the δ-neighborhoods of the two other edges, the triangle is called δ-slim.
If every triangle on a space has this property, then the space is also δ-slim. A metric space is hyperbolic, if there is a δ such that every triangle is δ-slim. This implies the existence of a global δ in hyperbolic spaces.
Our project had the aim to visualize the δ-neighborhoods for different triangles in the Poincaré disk model, to compute the minimal δ for different triangles, and to show how these minimal δ interplay with the global solution. In particular we implemented a function that returns whether a given triangle is δ-slim for a given δ.
It uses lines of constant distance to the edges – so called hypercycles – and their intersection points with the other edges of the triangle.

This enables us to approximate the minimal δ for which a given triangle is still δ-slim using the mentioned function and nested intervals.

Taking an experimental approach, we created a random sample of points uniformly distributed in the Euclidean unit circle.

From this sample we created random triangles with different amount of ideal points as vertices and plotted their minimal δ.
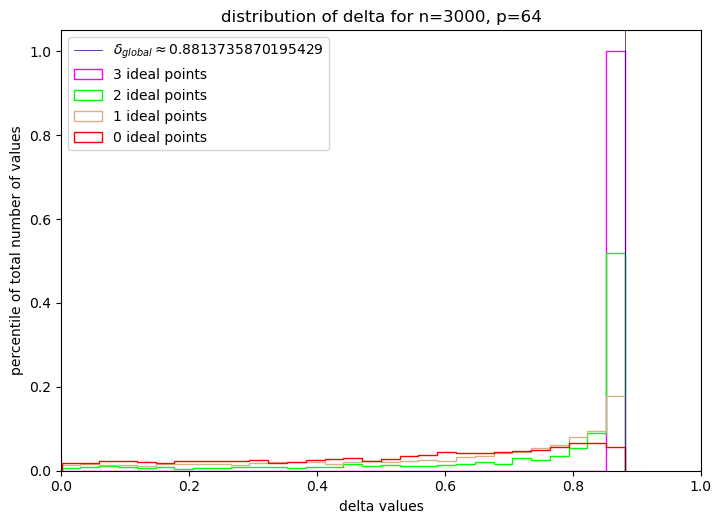
For more ideal points, more triangles have a greater minimal δ. We find a maximum of the minimal δ, a global δ, which is the same value that all of the ideal triangles yield: 0.881373587064445
Also, the analytical solution for this problem is \(\log\left(1+\sqrt{2} \right)\) (which is approximately equal to 0.8813735870195429). This result confirms our expectations. It is quite easy to show that every non ideal triangle is surrounded by an ideal triangle, and therefore if the ideal triangle is δ-slim the non ideal triangle is as well.

It is well established by the earlier mathematical work that all ideal triangles are congruent. So in conclusion, the minimal δ of any ideal triangle already is the global δ of the space.
As we know the upper half plane and poincare disk models are isomorphic, so we extended our code to the upper half plane model as well.

The accompanying code can be found on github and the image credits go to the blog post authors.
