Written by Isabel Giray, Karina Kniel and Phil Neitzel.
The goal of this project is to give an intuitive way of understanding the hyperbolic space. Inspired by the classic Ping-Pong game which is played in an Euclidean setting, the hyperbolic version visualizes the geometric differences.
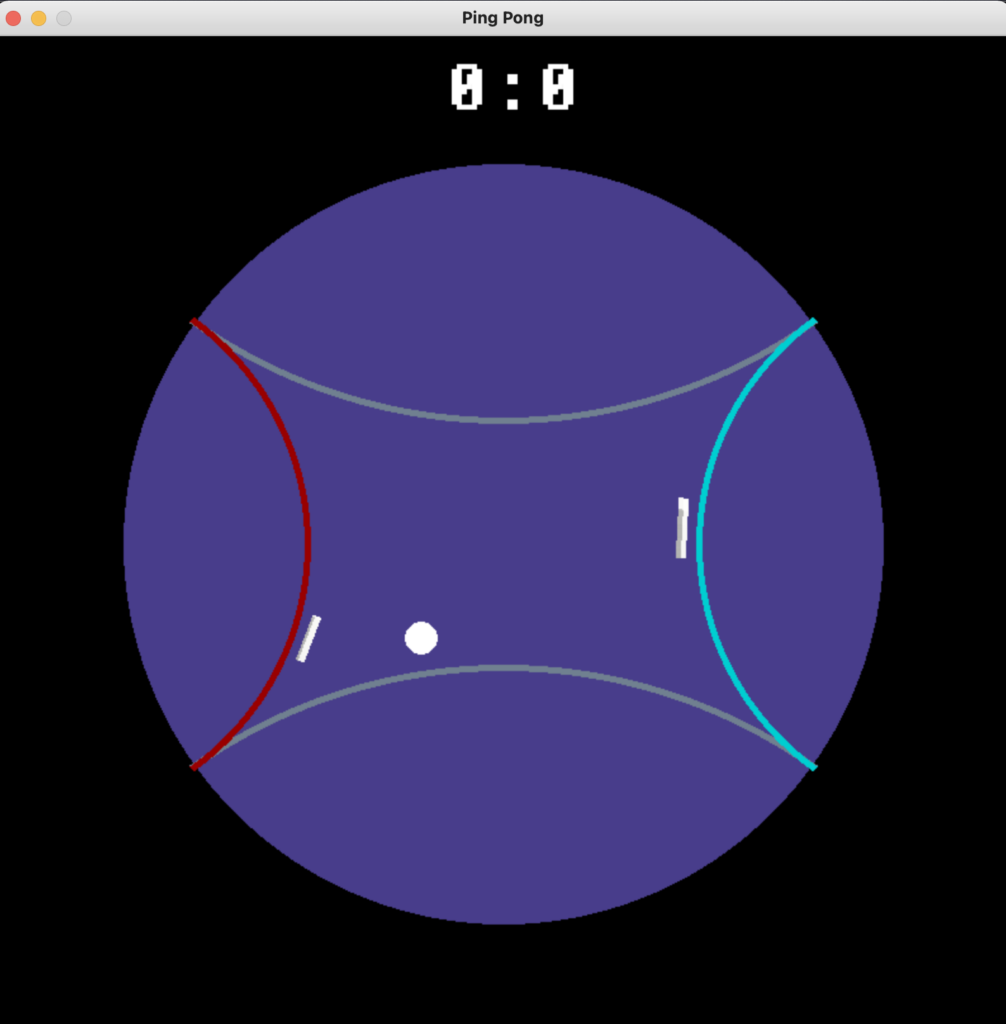
The game takes place on the Poincaré disc (as a set simply the unit disc in \(\mathbb{R}^2 \)) where the hyperbolic equivalent of a rectangle is our playing field. Straight lines are called geodesics in the hyperbolic geometry and will either form a circular arc perpendicular to the boundary of the Poincaré disc, or a diameter of the disc if the center of the Poincaré disc lays on the geodesic.
Therefore one of the most obvious changes is the movement of the ball. So in our intuitive Euclidean understanding it’s not as easy to predict the next impact point because the ball moves on above mentioned geodesics. Additionally, those can be recognized in the movement of the rackets.
Another property of hyperbolic geometry to be considered is the dependence of the distance regarding the position on the disk. The closer two points are to the boundary of the disc in an Euclidean sense, the greater their distance to each other becomes, hence the ball and the rackets have to change their size depending on their location.
The speed of the ball along a given geodesic is implemented as constant Euclidean speed. Adapted to hyperbolic properties, the ball would have to get slower towards the boundary of the disk as the distance from the origin grows larger. However we decided on constant Euclidean speed in order to make the game more fun. The only time the ball increases its speed is when one of the players scores a point.
Our game can be found on github and the two rackets used to hit the ball can be moved using: ”W”, ”S”, ”↑”, ”↓”. If you miss the ball, your opponent will get a point. Whoever gets five points first, wins. Enjoy!
A javascript version was also added to a website, so you can easily play it there now.
Notes by Ricardo: The javascript version of the original python code of this project was generated using pyjsdl-ts and a transcription software called transcrypt. After some rewrite of the python code to bring it into a required format, the transcription software, using pyjsdl instead of pygame, automatically generates the javascript code, which can easily be bound into a html webpage. The javascript and rewritten python code can be found on this github page. The readme file there also contains some notes on the generation of javascript code.
The original python code in general runs more smoothly, as the transcription is not ideal. Also, the substitution of pygame with pyjsdl-ts is not perfect, e.g. the boundary circles of the playing area do not overlap in the original python version.
