Written by Mara-Eliana Popescu.
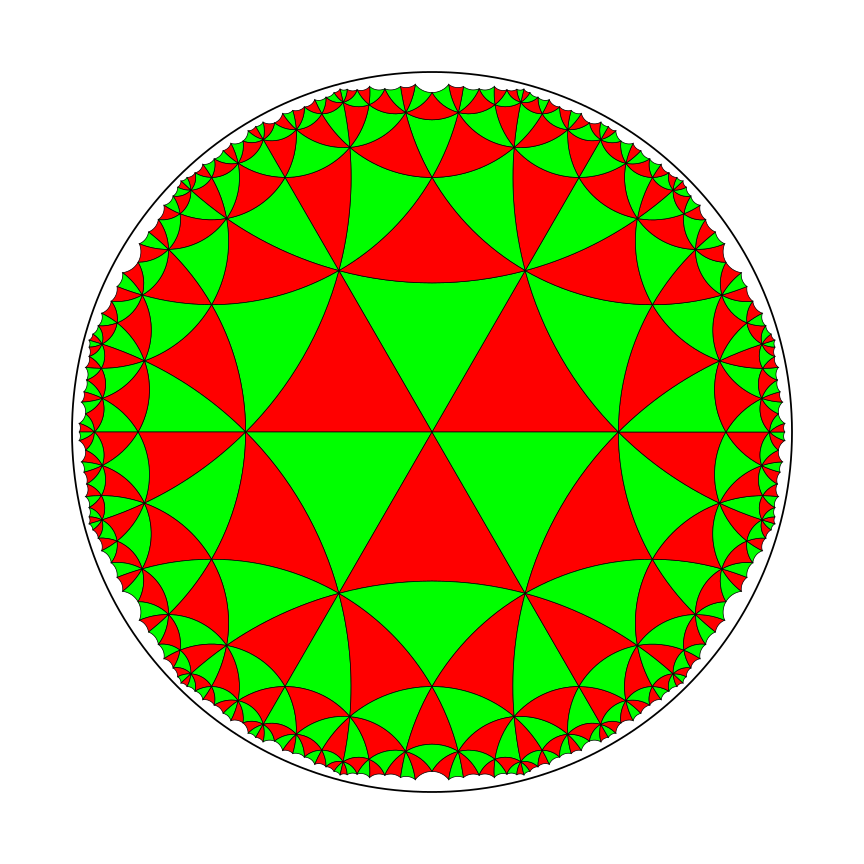
If asked to think of a tiling of the Euclidean Plane, surely many of us would imagine the pattern on a chessboard and perhaps some might try picturing a Penrose tiling. Such tessellations are well-known beyond a mathematical setting, whereas tilings of the Hyperbolic Plane are not as easily correlated with familiar images. The target of this project was to visualize a great number of hyperbolic tessellations on the Poincaré Disk (the unit disk in \(\mathbb R^2\)) using certain triangles as tiles, so called Möbius triangles. Much like in the Euclidean Plane, a tessellation of the Poincaré Disk consists of a set of tiles (e.g. regular polygons) aligned so that they fill up the disk completely, they do not overlap and no corner of one tile lies along the edge of another. The tiles that one can use for this purpose, as well as how they get aligned within the disk make up the difference between Hyperbolic and Euclidean tessellations.
First, let’s consider how the tiles generally look like in the hyperbolic setting and then, more specific, how one can obtain a non-overlapping tiling using triangles. It is important to know, that “straight lines” (also named geodesics), are redefined in the hyperbolic plane. A geodesic of the Poincaré Disk is either a circle arc orthogonal to the boundary of the disk or a Euclidean line going through the midpoint of the disk. In order to obtain a polygonal tile, one can choose a set of vertices within the plane and a set of geodesics that connect the vertices. Intuitively, not all such tiles can be aligned so that they do not overlap. Möbius triangles are an example of polygons that can generate a non-overlapping tiling. These triangles are described by three whole numbers \((p~q~r)\), which represent the angles \(\pi/p\), \(\pi/q\) and \(\pi/r\) at the vertices.
One method of aligning tiles on the disk relies at its core on a principle used for Euclidean tessellations as well: place a tile on the plane and then reflect it across its sides to obtain new neighboring tiles. Repeating this process for each tile leads to a tessellation of the plane. Since the Hyperbolic plane is endowed with a different metric than the Euclidean plane, a hyperbolic reflection will in most cases differ from a Euclidean reflection. In the Poincaré Disk, a reflection across a geodesic that is a circle arc is the same as a Euclidean inversion in the circle containing that arc. If the geodesic is a diameter of the disk, reflecting across it is the same as in Euclidean geometry.
By implementing the aforementioned elements and methods in a Python program, we managed to obtain tessellations of the disk with arbitrary Möbius triangles. As one might notice, the disk is not entirely filled with triangles. Close to the boundary, the triangles become very small and the time to generate an additional layer of tiles grows exponentially, which is why we limited the algorithm to create new triangles up to given point.