Independent Projects
Visualizing SubRiemanniann Billiards
Mentor(s): Lucas Dahinden, Lutz Hofmann, and Maksim Schreck
Student(s) participating: Jakob Niessner
Details: All the details are contained in this pdf.
Planimeters and Bicycle Tires
Mentor(s): Lucas Dahinden
Student(s) participating: Aaron Osburg
Details: Planimeters are devices used to measure the area of a region in the plane by tracing around its boundary. As such, they are a mechanical manifestation of Green’s Theorem. The goal of this project is to build models of the polar and of the hatchet planimeter and understand the mathematics behind them. The hatchet planimeter is connected to bicycle tire tracks and the project could further explore a conjecture by Menzin about their geometry using this planimeter. [blog post]
Laminations on Hyperbolic Surfaces in the Universal Cover
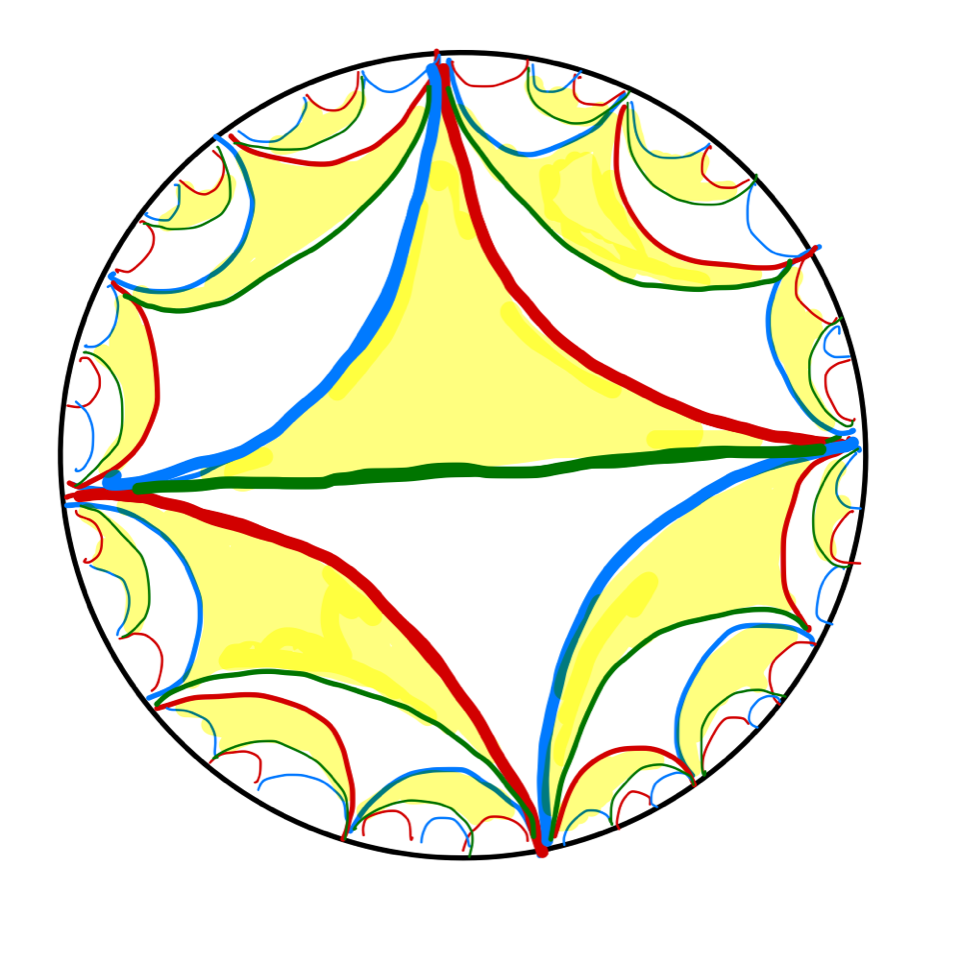
Mentor(s): Mareike Pfeil, Dia Taha
Student(s) participating: Christian Alber
Details: A lamination on a hyperbolic surface is a collection of simple disjoint geodesics whose union is closed. Laminations are very helpful when studying surfaces. For instance, they can be used to deform hyperbolic surfaces and to define coordinates on Teichmüller space. The goal of this project is to visualize lifts of laminations on hyperbolic surfaces in the Poincaré disk model for the hyperbolic plane.
Prerequisites: A first course in differential geometry, basic algebra, basic hyperbolic geometry will be needed, but can be learned during the project.
Geometric Constructions with the MIRA
Mentor(s): Denis Vogel
Student(s) participating: Silas Gramlich
Details: The MIRA is a semi-transparent reflective device used for constructing geometric objects. The goal of this project is to build such a device and understand the mathematics behind it.
SFB Funded Projects
Symplectic Billiards
Mentor: Peter Albers
Student(s) participating: Fabian Lander, Jannik Westermann
Details: The goal of this project is to simulate symplectic billiards on non-convex polygons, and to search for periodic orbits in particular.
Hyperbolic Billiards
Mentor: Dia Taha
Student(s) participating: Christian Alber, Mara-Eliana Popescu
Details: The project aims to investigate the statistics of hyperbolic billiards.
GitHub repository: link
Proseminar/Seminar Projects
Ping-Pong Game in the Poincaré Disk
Mentors: Brice Loustau, Anja Randecker, Ricardo Waibel and Mathias Häberle.
Students participating: Isabel Giray, Karina Kniel, Phil Neitzel
Details: The goal of this project is to implement a game inspired by the classic Ping Pong game, but in a hyperbolic setting. The game takes place in the Poincaré disc, only a finite area (the hyperbolic equivalent of a rectangle) is available to the ball. Players can move their racket along a fixed geodesic (a generalization of the concept of a straight line), and the ball obeys these different laws for its movement as well. Through the game players can then develop an intuitive understanding of hyperbolic geometry. [blog post]
GitHub repository: link
Delta-Slim Triangles in the Poincaré Disk
Mentors: Brice Loustau, Anja Randecker, Ricardo Waibel, and Mathias Häberle.
Students participating: Deniz Aydın, Simon Heidrich
Details: The delta-slim property of a triangle is defined as follows: take two sides of the triangle and draw a delta neighbourhood around them. Then check whether the third side lies completely in the union of the neighbourhoods. If this is true for all choices of two sides, then the triangle is called delta-slim. The project takes an experimental approach to firstly finding the minimum delta for a given hyperbolic triangle on the Poincaré disc, and secondly, to determine a minimum delta for all possible hyperbolic triangles on the Poincaré disc, i.e., a delta, for which all hyperbolic triangles on the Poincaré disc are delta-slim. [blog post]
GitHub repository: link
3D Prints of Tilings in the Poincaré Disk
Mentors: Brice Loustau, Anja Randecker, Ricardo Waibel, and Mathias Häberle.
Students participating: Helen Freytag, Ronya Ramrath
Details: Inspired by M.C. Escher’s works (especially Circle Limit I-IV), this project looks at tilings of the Poincaré disc and recreates their mathematical aspects as models using 3D printing. On top of that, the HEGL logo is adapted to a 3D model, whose components include geodesics and horocycles in the Poincaré disc. [blog post]
GitHub repository: link
Thingiverse: link
