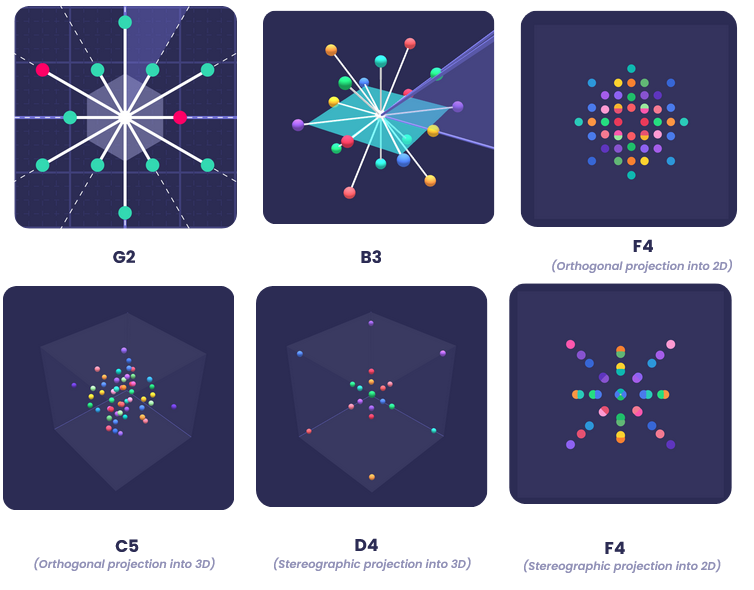
Written by Amelie Strupp Introduction This project aimed at providing an interactive application to visualize Root Systems and theircorresponding Weyl groups. The final version is available through the following link. Prerequisites This section introduces some important concepts by using visualizations…
Written by Noah Koopmann and Ingmar Lowack Due to the nature of our project, respectively the amount of subject-related text on our web application (see here), we will use the space of this blog post to talk about our work…
Written by Leon-Josip Dzojic, Matilde Sciortino, and Pirmin Kupffer In the year 1980 M. H. Freedman conjectured that every generic smooth knot in three dimensional Euclidean space has a tritangent plane, i.e., a plane tangent to three distinct points. However,…
Written by Ricardo Waibel in collaboration with Donald Youmans Topology and geometry are important concepts in mathematics and physics. Especially in theories like general relativity they have a direct impact, as the spacetime description of a system is already quite…
Written by Alassane Diagne and Ayşegül Peközsoy Möbius transformations are functions of the form \(T\colon \mathbb{C}\rightarrow\mathbb{C},\ T(z) = \frac{az+b}{cz+d}\) with \(a\), \(b\), \(c\), \(d\) complex numbers. We often associate the mapping \(T\) with the matrix \(T=\begin{pmatrix}a&b\\ c&d\end{pmatrix}\). If you look…
Written by Aaron Osburg Imagine you are planning your birthday party which will take place in Heidelberg Castle. You have a lot of friends, so you are not quite sure if the inner courtyard of the castle provides enough space…
Written by Helen Freytag and Ronya Ramrath. Inspired by Escher’s experimentation with hyperbolic art (and driven by the tempting availability of 3D printers in the clearly very well-funded experimental geometry lab), this project was concerned with extrapolating and printing the…
Written by Deniz Aydın and Simon Heidrich. It is easy to imagine how spherical triangles are “fatter” than Euclidean ones. Just like this, hyperbolic triangles look slimmer in comparison. Gromov used this property to generalize hyperbolic spaces. Imagine δ-neighborhoods of…
Written by Isabel Giray, Karina Kniel and Phil Neitzel. The goal of this project is to give an intuitive way of understanding the hyperbolic space. Inspired by the classic Ping-Pong game which is played in an Euclidean setting, the hyperbolic…
